Планирование и обработка результатов многофакторного эксперимента, страница 3

1.4.  Планы для квадратичных моделей

Вводные замечания

В этом разделе рассматриваются планы для моделей, имеющих вид

                                  (1.22) 

 

Общее число неизвестных  коэффициентов в модели (1.22) равно

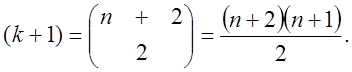                                                                                     (1.23)

 Для оценки коэффициентов модели вида (1.22), содержащей функции независимых переменных типа , независимая переменная в плане должна принимать по крайней мере три различных значения. Композиционный план для квадратичных моделей может быть получен путем добавления некоторого количества специальных точек к  «ядру». В качестве «ядра» могут быть использованы планы типа 2ⁿ  или 2^n-p. Если к ядру добавить точку в центре плана с координатами 0,…,0 и 2n так называемых «звездных точек» с координатами

                                  ( ,  0, …,0), …,(0, …,0, ),                                                      (1.24)

то получается  центральный композиционный план. Общее число (опытов) точек плана

                                                                N = 2ⁿ + 2n + 1.                                                           (1.25)

 На фиг.1.2 показаны точки  ортогональных композиционных планов для n = 2 (а) и n =3 (б).      

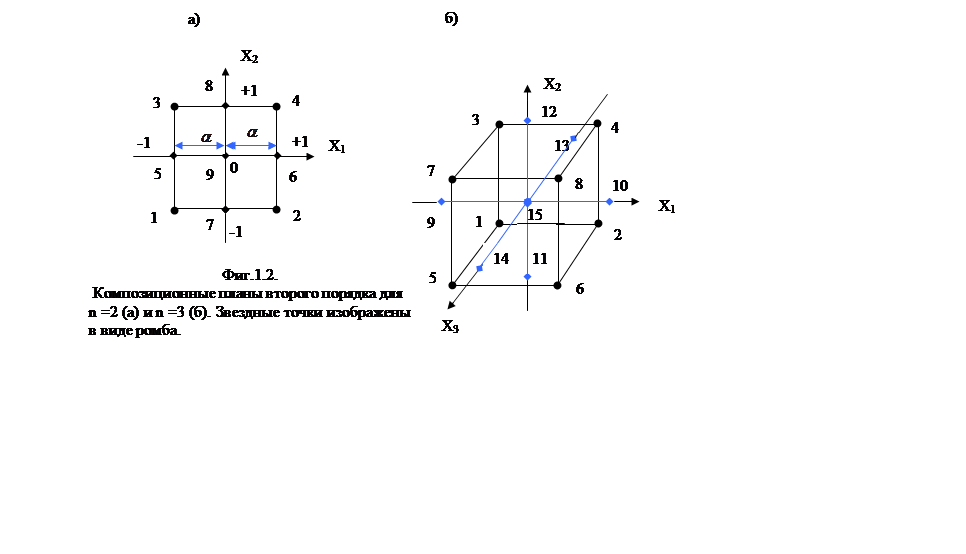
Ортогональные центральные композиционные планы (ЦКП).

     При построении этих планов величина  (плече звездных точек)  выбирается так, чтобы обеспечить ортогональность получаемого плана. Число точек в центре плана обычно принимается  равным единице. Для обеспечения ортогональности квадратичной модели (20) запишем ее следующим образом:

         (1. 26)

Здесь

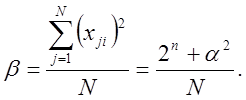                                                                                                             (1.27)

      В выражении (1.26) N – общее число точек в плане, 2ⁿ – число точек ядра композиционного плана. От модели (1.25) легко перейти к модели (1.22), определяя   в (1.22) следующим образом:

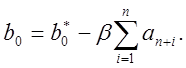                                                                                                                    (1.28)

Условие для выбора значения , обеспечивающего ортогональность плана:

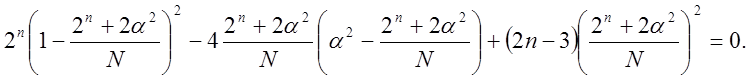                         (1.29)

Из этого следует

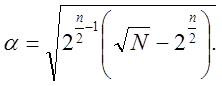                                                                                                                 (1.30)

Значения   в зависимости от числа факторов ( n ) приведены ниже

Число факторов	Ядро плана	N
2 3 4 5	22 23 24 25-1	9 15 25 27	1 1.215 1.414 1.546

Табл.1.1. Звездное плечо  как функция числа факторов.

2.1 Практическая часть

Задание

Составить план эксперимента химического процесса. Условия эксперимента, определяемые значениями факторов в отдельных опытах, записать сначала  в виде кодированных значений, а затем в натуральном масштабе факторов в матрицу планирования.  Используя размерную матрицу планирования эксперимента, провести имитационный эксперимент на модели химического процесса. Обработку результатов эксперимента провести на базе регрессионного анализа с использованием ППП “STATISTICA”.

2.2 Постановка задачи

 На практике встречаются процессы, характер протекания которых детерминированным образом зависит от определенных величин   .