Планирование и обработка результатов многофакторного эксперимента, страница 6

При расчете коэффициентов регрессии  и коэффициентовкорреляционной матрицы в анализ включить зависимую переменную (Y) и независимые (Х1, Х2, Х3, Х12, Х13, Х23). Новые таблицы с расчетными значениями коэффициентов регрессии и корреляции, как и в первом случае,  полностью переписать в лабораторный журнал.

2.7 Планирование эксперимента с учетом квадратичных эффектов

(ортогональный ЦКП)

Для описания химического процесса полиномами второй степени (2.5)  необходимо, чтобы независимые факторы принимали в плане не менее трех разных значений. ПФЭ 3³ будет содержать 27 опытов, что слишком много.

          (2.5)

 Поэтому воспользуемся ЦКП, где число опытов, рассчитываемых по формуле (1.25) равно 15. Из них 8 составляют ПФЭ  плана 2³ эксперимент по которому уже проведен и матрица в нормированных и в натуральном масштабе составлена.

       Достроим имеющийся план до ортогонального ЦКП путем добавления трех столбцов для кодированных переменных  (X₁₁ , X₂₂ и X₃₃)  и семь строк для опытов в звездных точках и в центре плана (с 9 – 15). Чтобы матрица планирования была ортогональна, нужно преобразовать уравнение (2.5) к виду:

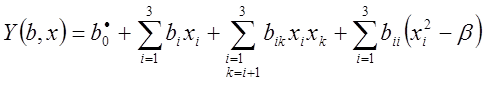                                                (2.6)

Матрица F  функций независимых переменных для ортогонального ЦКП имеет вид , показанной на фиг.2.2. Здесь номера опытов  соответствуют номерам точек на фиг.1.2 (б). Звездное плечо  (табл.1.1)  для  n = 3. Величина  рассчитывается по формуле (1.27),  а ;        ;       .

	Номер опыта j	Матрица F
		Матрица X плана			X12	X13	X23	X11	X22	X33
Ядро плана (2n)	1 2 3 4 5 6 7 8	-1 +1  -1 +1  -1 +1  -1 +1	-1  -1 +1 +1  -1  -1 +1 +1	-1 -1 -1 -1 +1 +1 +1 +1
Звездные точки         (2n)	9 10 11 12 13 14	0 0 0 0	0 0 0 0	0 0 0 0
Центр плана  (n0)	15	0	0	0	0	0	0

                       Фиг.2.2. Композиционный план второго порядка для n =3

После заполнения матрицы F рассчитать размерную матрицу планирования для  семи опытов и по их значениям провести дополнительный эксперимент по алгоритму описанному выше. Полностью заполненная таблица данных должна быть сохранена. Регрессионный и корреляционный анализ провести с учетом всех факторов матрицы F. Новые таблицы с расчетными значениями коэффициентов регрессии и корреляции, как и в первых двух случаях,  переписать в лабораторный журнал.

2.8 Интерпретация полученных моделей по результатам регрессионного и корреляционного анализа

Задача интерпретации  установление в какой мере каждый из факторов влияет на целевую функцию (функцию отклика Y). Для этого надо сравнить корреляционные зависимости для трех моделей химического процесса. Проверить на значимость коэффициентов  уравнений регрессии. Незначимые коэффициенты из уравнений регрессии исключить. Факторы, коэффициенты которых незначимы, естественно не интерпретируются. Заключительным этапом  является принятие решения по выбору наилучшей модели химического процесса: линейной, линейной с эффектами взаимодействия (неполной квадратичной) и квадратичной. Кроме перечисленных факторов выше, модель та лучше отражает свойства исследуемого химического процесса, которая имеет наименьшую погрешность и высокий коэффициент детерминации.