Решение задач наиболее часто встречающихся на практике при проектировании систем распределения информации, страница 4

Вывод: В этой задачи мы рассмотрели систему с ожиданием вызова для  случайного времени обслуживания вызова и для постоянного времени построили кривые зависимости , из которых можно сделать вывод, что вероятность ожидания с выше допустимого времени для любого поступившего вызова и вероятность ожидания для задержанного вызова уменьшаются с увеличением времени. При чем при случайном времени обслуживание спад кривой более пологий чем при постоянном времени. Так же вероятности для постоянного времени обслуживания меньше чем для  случайного. Это можно объяснить тем что при постоянной длительности нагрузка от абонентов меньше, так как время обслуживания маркером абонента постоянна, при случайном времени ситуация противоположна.   

Задача № 6

На вход ступени ГИ АТС поступает нагрузка по двум пучкам линий, математическое ожидание которой y₁ и y₂. На выходе ступени объединенная нагрузка распространяется по направлениям пропорционально коэффициентам К_i. Определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам расчета сделать вывод.

Исходные данные:

у1=40 Эрл

у2=40 Эрл

                     К1=0.15

К2=0.25

К3=0.6

Решение:

Входная объединенная нагрузка

увх=у1+у2=40+40=80 Эрл

Г И

                                                          

                                                             

          Y₁                                     

                                                              

                                                             

            Y₂

                                                             

Определим значение нагрузки каждого направления:

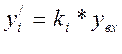
 Эрл

Эрл

Эрл

Переведем нагрузку каждого направления в расчетную нагрузку:

ур1=14.3 Эрл

ур2=23 Эрл

ур3=52.7 Эрл

Определим относительное отклонение расчетного значения нагрузки от ее математического ожидания используя формулу:

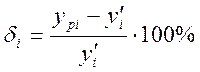
δ1=19.1%

δ2=15%

δ3=9.8%

Вывод:

          С увеличением среднего значения нагрузки относительное отношение рассчитанной нагрузки от ее математического ожидания уменьшается. Это связано с нелинейной зависимостью Y_р от Y. Чем больше группа источников, тем меньше колебание нагрузки, поэтому отличие между Y_р и Y  следует учитывать при расчете систем, работающих с небольшой нагрузкой.   

Задача №7

          Требуется построить коммутационное поле с N входами и M выходами, работающее в режиме линейного искания. Удельная нагрузка на один вход составляет:  а, Эрл. При этом необходимо рассмотреть два варианта структуры КП.

1)  четырехзвенная схема (Z=4) с блочной структурой, построенная итерационным способом из двухзвенной схемы путем замены каждого коммутатора звена А на двухзвенный блок АВ имеющий   входов,  выходов, связность  и  входов в один коммутатор звена А, а каждого коммутатора звена В на двухзвенной блок CD, имеющий  входов,  выходов, связность ; связность между входами блока АВ и входами блока CD равна ;

2)  трехзвенная односвязная схема (Z=3) неделимой (связной) структурой, имеющая на звене А коммутаторы с  входами, а на звене С коммутаторы с таким же число выходов .

Число коммутаторов на звене В трехзвенной схемы построения КП необходимо подобрать таким образом, чтобы рассматриваемые варианты структуры имели приблизительно одинаковую вероятность внутренних блокировок. Вычертить соответствующие схемы группообразования при Z=3 и Z=4. Выбрать более предпочтительный вариант построения КП, используя в качестве критерия сравнения объем оборудования (число точек коммутации) на единицу обслуживаемой нагрузки.

Исходные данные:

N	M	а, Эрл	Z=3 na=mc	nab	mab	Z=4 na	ncd	mcd	mD	fcd	fab	fbc
225	900	0.31	9	45	90	5	50	100	20	2	1	2

Решение:

                    Чем больше звеньев, тем строить поле выгоднее, при тех же условиях, для уменьшения внутренних блокировок.