Решение задач наиболее часто встречающихся на практике при проектировании систем распределения информации, страница 2

На полнодоступный пучок из V линий поступает простейший поток вызовов с интенсивностью  вызовов в час(C), длительность занятия линии одним вызовом распределена по эксподенциальному закону со средним значением t, обслуживание вызовов осуществляется по системе с явными потерями. Определить:

1.  математическое ожидание числа вызовов поступивших за время t (M(k))

2.  определить вероятности всех возможных состояний пучка линий  отличающихся числом занятых линий и построить зависимость

3.  Вычислить математическое ожидание занятых линий M(i)

4.  найти вероятности потерь по времени, нагрузки, вызовам:

Расчет для 2-4 повторить для примитивного потока.

          Исходные данные:

                             μ=с=200

                             t=100

                             v=12

                            N=18

 Решение.

Расчет начнем с того, что определим нагрузку:

Y=c*t/3600=200*100/3600=5.55 Эрл

           - представляет математическое ожидания числа вызовов:

M(k)= =200*100=20000

          Вероятность всех возможных состояний определяем в соответствии с первой формулой Эрланга: 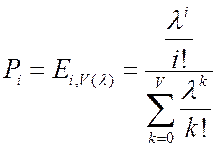, она используется когда полнодоступная схема. Это вероятность того, что в обслуживаемой системе занято точно V линий. Так же можно использовать рекуррентные формулы: 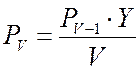. Рассчитаем с помощью MathCAD эти вероятности. Для простейшего пучка: .

P₀ – P₉ = 0

P₁₀  = 3.1 * 10^-3

P₁₁ = 0.056

P₁₂ = 0.94

-  вероятность того, что нет занятых линий.

- вероятность того, что все 15 линий заняты.

          Для простейшего потока: .

          Вычислим  математическое ожидание  числа занятых линий:  

     Рассчитаем по той же схеме для примитивного потока. Вероятность занятия всех линий в пучке обслуживающих примитивный поток, определяется по формуле Энсета: 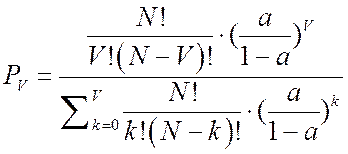, где

a - удельная нагрузка от одного источника нагрузки.

.

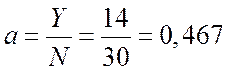Рассчитаем вероятности занятия линий:

P₀  - P₄ = 0

P₅ = 1.2 * 10^-3

P₆ = 5.2 * 10^-3

P₇ = 0.015

P₈ = 0.049

P₉  = 0.12

P₁₀ = 0.197

P₁₁ = 0.286

P₁₂ = 0.334

Для примитивного потока: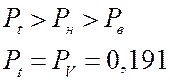

Вероятности потерь по нагрузки: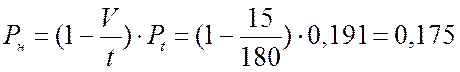

Вероятность потерь по вызовам: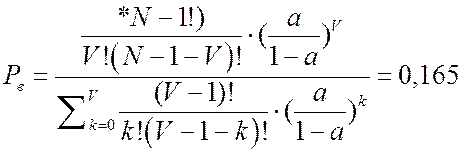

Кривые распределения P(i)

 

Вывод: В этой задачи мы изучили потери в системах с явными потерями. Рассчитали математическое ожидание числа вызовов поступивших за время t, и мат. ожидание числа занятых линий. Рассчитали вероятности потерь по времени, по вызовам, по нагрузки.  Построили графики зависимости P=f(i). Из графиков видно, что у простейшего потока вероятность занятости малого числа линий близка к нулю и почти единица при занятии всех линий. У примитивного потока эта зависимость более менее гладкая.

Задача 4

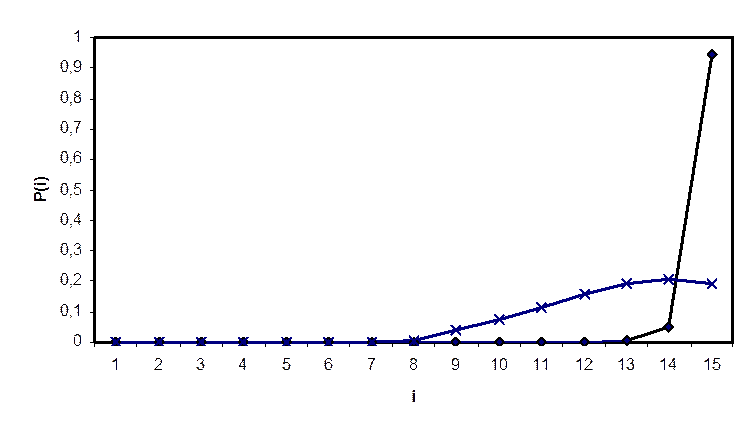В рассматриваемом направление ступени ГИ из g блоков поступает нагрузка , а нагрузка на входы всей ступени ГИ  составляет доступность равную q. Вероятность потерь p=0,005. Определить требуемое число линий в направлении при установки на ступени блоков:

1.  ГИ-3 (80*120*400)

2.  ГИ-6 (60*80*400)

Исходные данные:

      g=6

 q=2

          Yм=64

          Yги=380      

     Решение.

Для ГИ-6 (60*80*400), на МКС 10*20*6

                          

Количество МКС: 60/10=6 в звене А, 80/10=8 в звене Б.

Количество коммутаторов(k): 80/20=4 в звене А, 400/20=20 в звене Б.

Число входов в один коммутатор(n): 60/4=15 – А, 80/20=4 – Б.

Число выходов из одного коммутатора(m): 80/4=20 – А, 400/20=20 – Б.

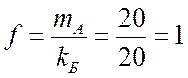 - односвязный блок.

Так как 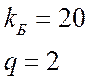, то  - max доступность.

          Min доступность:

Значит: .

          Нагрузка на один блок: Yбл=Yги/g=380/8=47.5

a=Yбл/Na=47.5/60=0.79 - удельная нагрузка на один вход, тогда нагрузка обслуживаемая одним коммутатором звена А:Ym=a*na=0.79*15=11.85.

=q*(ma-Ym)=2(20-11.85)=16.3- средняя доступность (мат. ожидание).

12+0.725(16.3-12)=15.11.

           - эмпирический коэффициент учитывающий блокировки. 

По таблицам определяем  и находим необходимое число линий:

ά=1.42

β=4.6

V=α*Yм+β=1.42*55+4.6=83

          Тем же способом рассчитываем для ГИ-3 (80*120*400) на МКС 20*20*3

Количество МКС: 80/20=4 – А, 400/20=20 – Б,