Другие предметы \ Теория телетрафика

Решение задач наиболее часто встречающихся на практике при проектировании систем распределения информации, страница 3

K: 120/20=6 – А, 400/20=20 – Б,

n: 80/6=13 и 14 – А, 120/20=20 – Б,

m: 120/6=20 – А, 400/20=20 – Б.

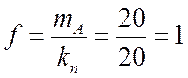
Dmax=40

Dmin=(20+1-14)*2=14

14<Dэфф<40

Yбл=47.5

a=47.5/80=0.6

Ym=0.6*14=8.4

=2(20-8.4)=23.2

Dэфф=14+0.725(23.2-14)=20.67

α=1.3

β=5.6

V=α*Yм+β=1.3*55+5.6=77

Схема блока ГИ – 6 (6 блоков (g=6)).

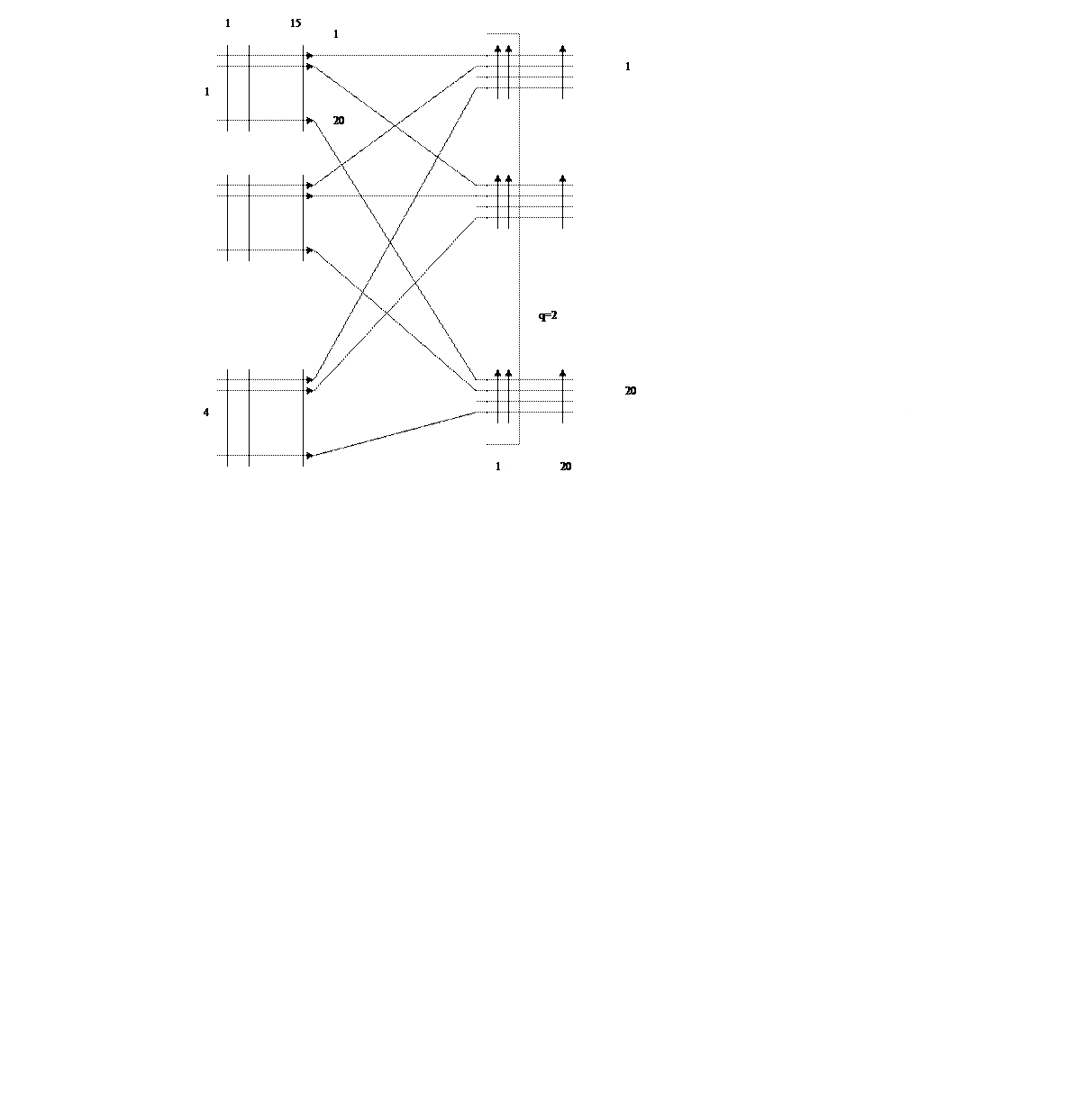
Схема блока ГИ – 3 (6 блоков (g=6)).

         Вывод: Решая эту задачу мы рассчитали  требуемое число линий в направление при установки  на ступени блоков ГИ – 3 и ГИ – 6. Рассчитали параметры этих блоков, построили их в сетчатом виде. Из результатов можно сделать вывод, что при прочих одинаковых условиях (одинаковой поступающей нагрузки, одинаковом числе блоков и т. д.), число линий оказалось разным: для ГИ – 6 V = 78;

                                для ГИ – 3 V = 76, значит при установки блоков ГИ – 3 выигрыш в 2 линии, что незначительно, это можно объяснить тем, что число пром. линий одинаково.

Задача 5

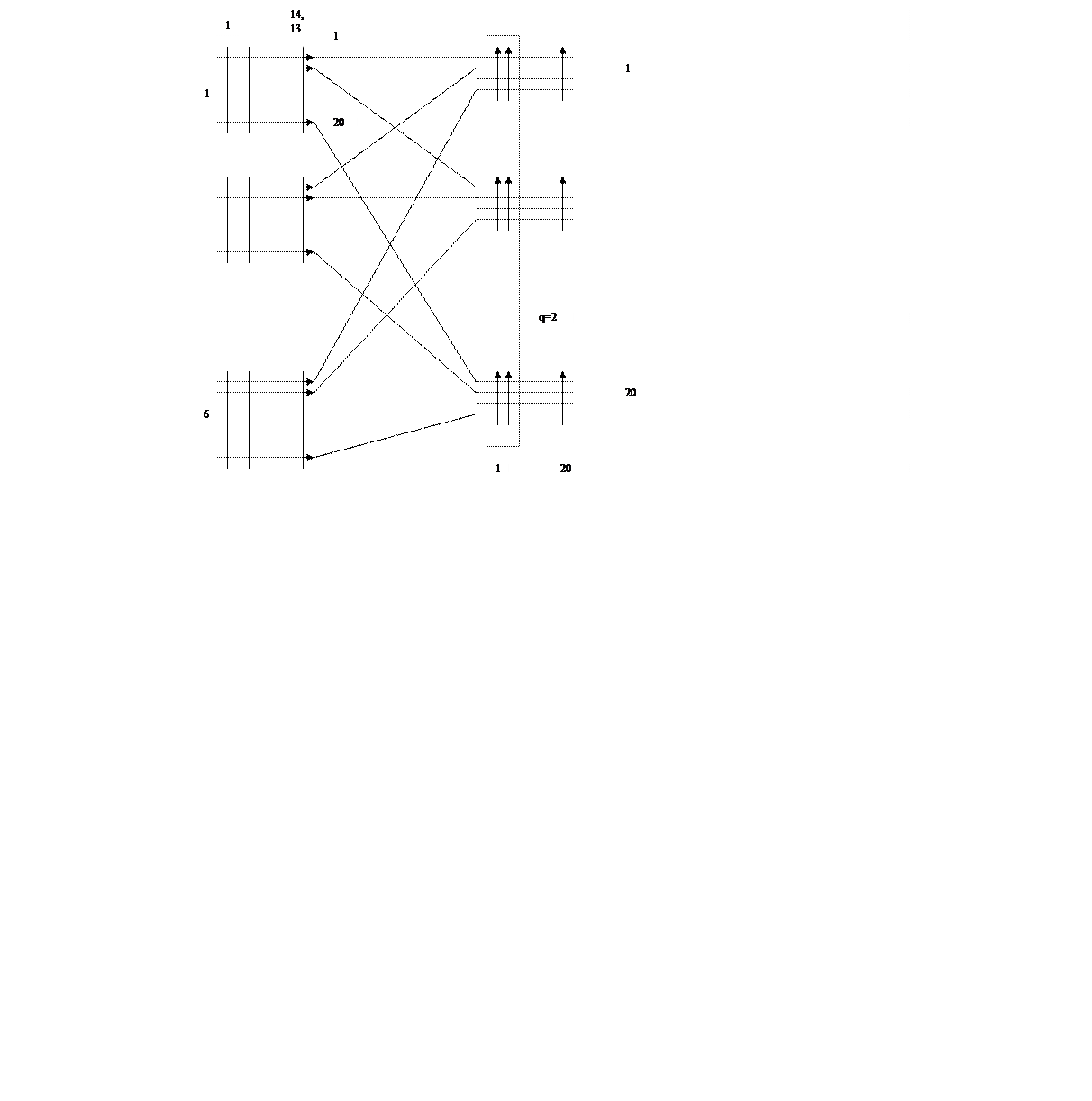
          На ступени ГИ координатной АТС установлено g  блоков, каждый из которых обслуживается маркером. На все входы поступает  нагрузка  при средней длительности занятия - . Маркеры работают по системе с ожиданием, затрачивая на обслуживание одного вызова h сек.. Требуется определить качественные показатели работы маркеров при постоянной и экспоненциально распределенной длительности обслуживания:

1.  вероятность ожидания  для поступившего вызова;

2.  вероятность ожидания  с выше доступного времени для любого поступившего вызова;

3.  вероятность ожидания  с выше доступного времени для задержанных вызовов;

4.  среднее время ожидания для любого поступившего вызова  и для задержанных вызовов ;

5.  среднее число ожидающих вызовов при экспоненциальном распределении (среднюю длину очереди);

6.  построить , при постоянной и экспоненциальной длительности обслуживании.

 Исходные данные:

 g=6

tвх=84

Yвх=221

h=0.64

t*1=0.64

t*2=1.28

t*3=1.92

Решение: простейший поток с показательно распределенной длительностью обслуживания – это значит с экспоненциальной, так как случайная длительность обслуживания.

          Простейший поток с постоянной длительностью занятия  значит со средней длительностью обслуживания .

           - выражает вторая формула Эрланга.

           определим из следующего соотношения: .

Рассчитываем при числе линий V = 1:

Yн=(h*Yбл)tвх=(h*Yвх)/(tвх*g)=0.64*221/84*6=0.28 Эрл

P(γ>0)=Pi=Yн=0.28 Эрл - вероятность ожидания для поступившего вызова.

          Рассчитаем вероятности ожидания с выше допустимого времени  для любого поступившего вызова:

P(γ>t*1)==0.28exp-(1-0.28)1=0.14

P(γ>t*2)=0.28exp-(1-0.28)2=0.07

P(γ>t*3)= 0.28exp-(1-0.28)3=0.03

          Вероятность ожидания для задержанного вызова:

 P(γз>t*1)= P(γ>t*1)/ P(γ>0)=0.14/0.28=0.5

P(γз>t*2)= P(γ>t*2)/ P(γ>0)=0.07/0.28=0.25

P(γз>t*3)= P(γ>t*3)/ P(γ>0)=0.03/0.28=0.11

P(j3 > 0) = 0.28

          Среднее время ожидания для любого поступившего и для любого задержанного вызова:

0.28/(1-0.28)=0.39с

Математическое ожидание числа вызовов ожидающих начало обслуживания:

M(j)= P(γ>0)*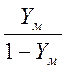=/(1-0.28)=0.11 

          Выше рассчитано для случайного закона распределения. Теперь рассчитаем для постоянной длительности обслуживания.

          Качественные показатели для этого случая определяются по кривым Кроммелина, для упорядоченной очереди обслуживания. А для случайной – по кривым Беркам.

P(γ>0)=Yм=0.28

              Рассчитаем вероятности ожидания с выше допустимого времени  для любого поступившего вызова:

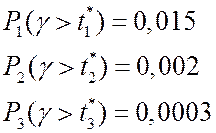               по таблицам.    

           P(j > 0) = 0.28

Вероятность ожидания для задержанного вызова:

P(γз>t*1)= P(γ>t*1)/ P(γ>0)=0.015/0.28=0.05

P(γз>t*2)= P(γ>t*2)/ P(γ>0)=0.002/0.28=0.007

P(γз>t*3)= P(γ>t*3)/ P(γ>0)=0.0003/0.28=0.001

0.28/(1-0.28)2=0.19с

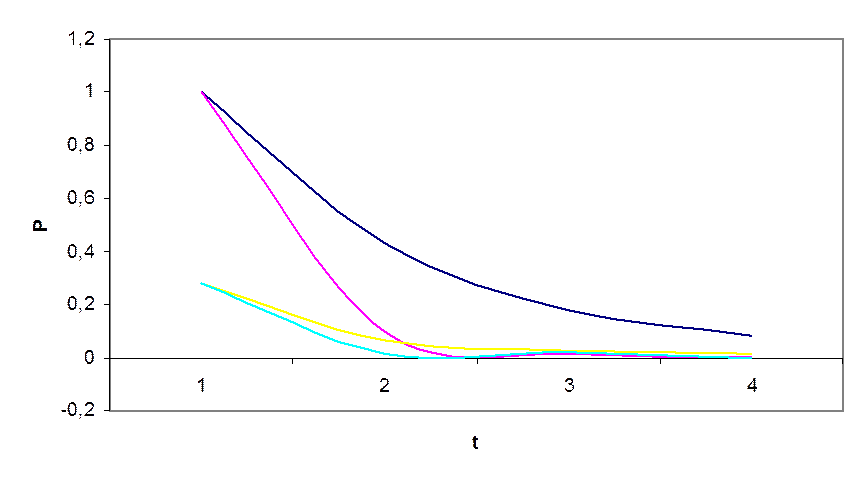
Построим графики зависимости: .

Для простейшего потока с показательно распределенной длительностью:

Скачать файл