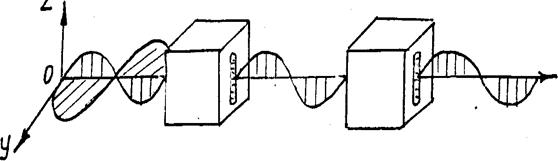
А теперь представим, что к прибору подойдут две поперечный волны с различными плоскостями колебаний (рис. 19). Через прибор пройдет только та волна, у которой плоскость колебания, как указывалось, совпадает с плоскостью щели, колебание в которой будут идти в одной плоскости. Такую волну называют плоско поляризованной, а прибор - поляризатором.
Если волна невидима, то поляризованную волну можно легко узнать, если воспользоваться ещё одним таким же прибором - анализатором (рис. 20)
При повороте такого прибора, как указано на рисунках, мы заметим, что при совпадении щелей поляризованная волна проходит, а когда плоскости щелей перпендикулярны, то волна задерживается вторым прибором.
Опыты показывают, что электромагнитные волны поляризуются, значит, они поперечны.
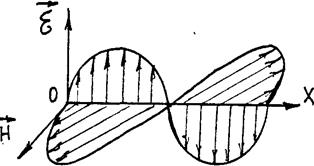
Плоскость колебания Е принято считать плоскостью колебания, а плоскость колебания Н плоскостью поляризации (рис. 21).
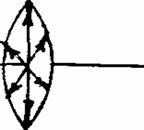
Световые волны обычно не представляют
асимметрии относительно луча, т.е. в естественном свете имеют место волны с
самыми различными плоскостями колебания (рис. 22) источником света являются
атомы, которые в любом источнике света огромное количество. Если луч света
пропустить через поляризатор, то произойдет поляризация света.
 |
|||||
 |
|||||
|
|||||
Поляризаторами являются кристаллы с анизотропией поглощения. Таким кристаллом может служить турмалин, кварц и т.д. Поляризацию света легко обнаружить, если использовать два таких кристалла. При повороте анализатора (рис. 23) мы заметим, что свет при одном его положении проходит через оба кристалла, при другом - гасится.
Поляризация света говорит о том, что световые волны поперечны.
Частичная поляризация наблюдается при отражении и преломлении света.
Большой интерес представляет вращение плоскости поляризации некоторыми веществами. Если между анализатором и поляризатором поместить сосуд с раствором сахара, то можно заметить, что плоскость колебания повернулась. По углу поворота можно определить концентрацию сахара в растворе.
Поляризация света дает дополнительные сведения об окружающем нас мире. Кроме того, она имеет практическое применение. С помощью ее определяют содержание в растворе некоторых веществ, изучают напряжения, возникающие в деталях при деформациях, используют для записи звука в кино и т.д.
1 Принцип суперпозиции волн
Возбудим в волновой ванне одновременно две одиночные волны (рис. 1). Наблюдая за ними, мы увидим, что каждая волна движется независимо от другой, будто второй волны нет.
Экспериментально установлено, что для волн с небольшими амплитудами справедлив принцип суперпозиции и при наложении волн результирующее смещение равно сумме смещений, вызываемых каждой волной в отдельности:
х = х1 + х2.
2. Интерференция волн
Допустим, что имеем два вибратора поперечных синусоидальных волн S1 и S2 (рис. 2), которые возбуждают колебания в точке К, расположенной от вибраторов на расстоянии с d1 и d2. Допустим, что колебания вибраторов S1 и S2 совпадают по фазе и имеют одинаковую амплитуду и частоту. Найдем результирующее смещение точки под действием дошедших до нее волн. Так как
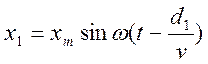
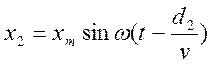
то
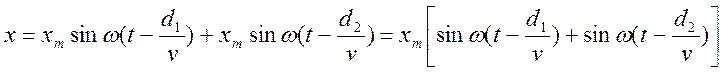
применим к сумме синусов формулу
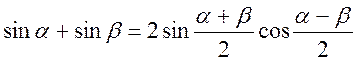
получаем
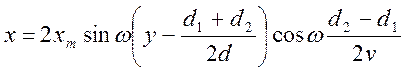
Постоянную величину 
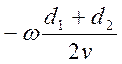обозначим через φ.
Тогда:
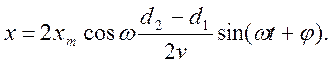
Отсюда видно, что амплитуда колебаний результирующего смещения
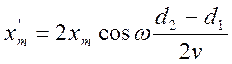
Зависит от разности расстояний d2-d1. которою принято называть разностью хода волн. Если разность хода волн составляет четное число 2k полуволн
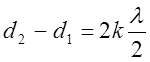
то
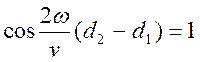
и амплитуда результирующих равна удвоенной амплитуде колебаний в каждой из волн:
.
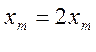Если же разность хода составляет нечетное число полуволн
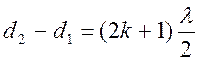
то
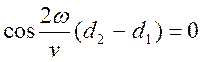
амплитуда результирующей волны равна нулю:
хm = 0.
Справедливость полученного результата легко, проверить на опыте. Для этого возбудим на поверхности воды две системы волн с одинаковыми частотами и амплитудами. Мы увидим картину, изображенную на рисунке 3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.