Интерференция волн. Дифракция волн. Дифракция света. Дифракционная решетка. Дисперсия волн, типы спектров, спектральный анализ, страница 2

В этом случае колебания усиливают друг друга. Так как синус функция периодическая, то явление усиления будет при ∆f = 0, 2π, 4π и т.д.

2 Пусть оба колебания имеют одинаковый период, но разность фаз ∆f = π (рис. 3) При сложении колебаний замечаем, что амплитуда результирующего Рисунок 1.колебания Хо = Хо₁ – Хо₂. Если Хо₁ = Хо₂, то колебания гасят друг друга, т.е. Хо=0.

Периодичность функции синус позволяет и здесь утверждать, что гашение или минимум колебаний наблюдается при ∆f = π, 3π, 5π и т.д.

Интерференция волн

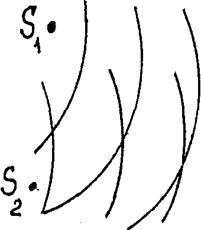
Допустим, что в упругой среде распространяются волны от двух источников. В области наложения волн частицы вещества должны принимать участие в двух колебаниях (рис.4) Результирующее колебание частиц будет находиться путем сложения колебаний. Допустим, что источники имеют одинаковую частоту, а разность фаз колебаний в любой точке остается постоянной. При сложении колебаний в некоторых точках будет наблюдаться усиление колебаний, в других -гашение их.

Как указывалось выше, максимум колебаний будет при ∆f = 0, 2π, 4π, ±2nπ, а минимум при                   

∆f = π, 3π, /2n+1/π, n=0, 1, 2, 3.

Из уравнения волны

y₁ = у₀sin(ωt - kх₁ + f₀) и у₂ = sin(ωt – kх₂ + f₀)

Найдем разность фаз

∆f = ωt – kх₁ + f₀ - ωt + kх₀ – f₀ = k(х₂ + х₁ )

Договоримся, что

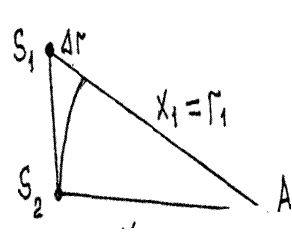
х₁=r₁ и х2=r₂ (рис.5).

Величину r называют ходом волны. Учитывая это,

∆f= k(r₂- r₁ )=k∆.

Величина К = 2π/λ, тогда ∆f=2π∆r/λ.

Учитывая это, находим, что максимум наблюдается при

2π∆r/λ = 2πn = ∆r =2πλ/2, где n = 0,1,2,3…

Усиление колебаний наблюдается в тех точках, для которых разность хода лучей равняется четному числу полуволн. Гашение волн наблюдается, если

2π∆r/λ = (2n +1)π = ∆r =(2π+1), где n = 0,1,2,3...

Гашение колебаний наблюдается в тех точках, для которых разность хода волн равняется нечётному числу полуволн.

При условии когерентности волн /постоянство разности фаз картина усиления и гашения волн будет устойчивой и называется интерференционной.

Интерференция света

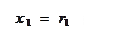
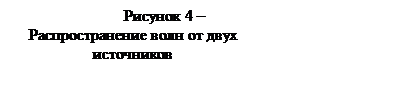
Так как свет представляет электромагнитные волны, то должна наблюдаться интерференция света. Нужно лишь получить когерентные волны.

На практике трудно изготовить два когерентных источника света. Источником излучения световых волн являются атомы. В любом даже очень малом источнике света «светящихся атомов огромное количество и сделать так, чтобы они излучали кванты света синхронно возможно лишь при строго определенных условиях, тем более, что переходы электронов с одних орбит на другие носят случайный характер.

Поэтому для наблюдения интерференции проще получить два световых потока от одного источника и направить их так, чтобы они пересекались. Такие пересекающиеся потоки можно создать, например, с помощью бипризмы Френеля (рис. 6).

Бипризма преломляет лучи так, как будто они идут не от одного, а от двух источников S₁ и S₂. Совершенно очевидно, что эти источники и волны должны быть когерентными. При наложении волн на экране получится типичная картина усиления и гашения волн, т.е. интерференция.

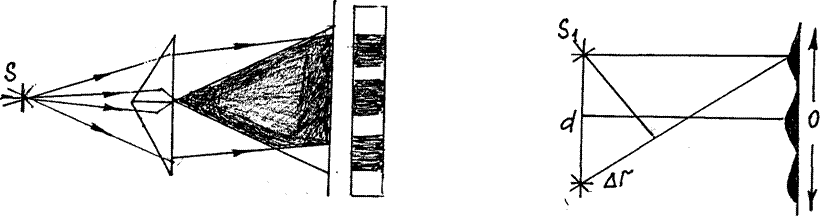
Расстояние между когерентными источниками (рис. 7) обозначим d. Если из середины отрезка d восстановить перпендикуляр до пересечения с экраном, то получим точку О. Разность хода волн до этой точки всегда будет равна нулю

∆r = 0 значит, в этой точке будет всегда наблюдаться максимум. Его называют нулевым максимумом.

 

	Рисунок 7 - Интерференция

 

По мере удаления от точки О, как указано на чертеже, ∆r начнет возрастать, что приведет к чередованию максимумов и минимумов. Для тех точек, где

∆r = 2nλ/2 наблюдается усиление, а в тех точках где ∆r = (2n+1) λ/2 будет гашение колебаний.