|
|
для скважин внутренних рядов. В рассматриваемом случае область дренирования D имеет вид параллелепипеда (рис. I), т.к. скважины несовершенные по степени вскрытия.
Для определения падения давления в скважине нужно решить уравнение пьезопроводности для области D . Верхняя и боковые границы области принимаются непроницаемыми. На нижней граница задается давление, равное начальному пластовому давлению, ^о отвечает условию напора по-дошвенных вод. Решение получено методом функций Грина. Функция Грина для уравнения пьезопроводности есть то давление, которое вызывается в точке М (X, Y,Z) пласта в момент -Ьдействием мгновенного источника единичной мощности, помещенного в точку м'(Х', У', Z1 ) в момент Z . При этом полагается, что начальное давление равняется нулю, а на границах выполняются однородные (т.е. нулевые) граничные условия.
|
К |
Если для уравнения пьезопроводности найдена функция Грина &■ (М, М ,М\Ъ-Ъ), то может быть определено падение давления в точке М в момент t ДР(М, t ). Функция Грина для исходной задачи тлеет вид:
где ^22^' Хс; * "^ ) и £"22^ ^ • ^ с' ^ "^ Функции Грина соответственно для бесконечной галереи X = Хс в полосообразном пласте с непроницаемыми границами X =.0 и X = 1( и такой же галереи У = Ус с граница-миУ=0иУ=У^ ; & 12^ * ^ с' ^ ~ ^ ) - функция Грина для галереи Z = 2 с в пласте, на нижней границе которого задано постоянное давление Р = Рдд^ , а верхняя граница непроницаема. Функции Грина для подобных одномерных задач были получены М.А.Гусейнзаде (1972).
|
h=o,< |
 Для рассматриваемых граничных условий падение давления в точке М определится выражением:
Для рассматриваемых граничных условий падение давления в точке М определится выражением:
|
(2) |
dZ
где Dc - область источника, дренирующегопласт; (f = = Qc/fi ~ дебитединицыдлины скважины; 3 - величинавскрытиялласта; J5* - коэффициент упругоемкости.
Окончательное выражение дляпадениядавлениявскважинеполученовбезразмерныхвеличинах. Значениебезразмерно! депрессиирассчитановшироко) диапазонебезразмерныхпараметров
|
|
|
Kt |
. _ h.
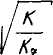
Ь*' = ■
|
h |
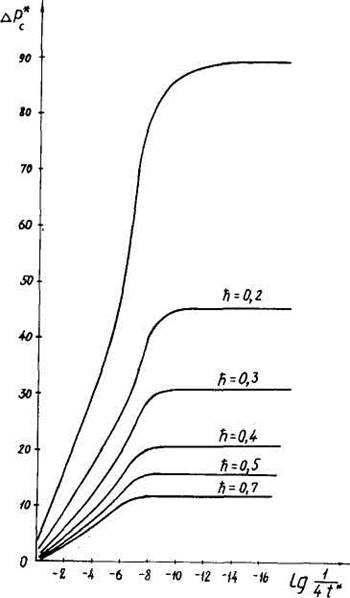
Рис. 2. Изменениебезразмернойдепрессиивнесовершеннойскважинепри
|
(3) |
S* = 1000
15
где S - площадь дренируемой области. Величина ,5 полагалась равной 200*200 м при расположении скважины в центре области дренирования. На рисунке 2 показано изменение безразмерной депрессии лРс для Ь*= iooo.
По результатам расчетов можно сделать следующие выводы.
С увеличением мощности пласта h или увеличением анизотропии темп падения увеличивается за счет влияния непроницаемых границ области дренирования (интерференции скважин).
Присутствие подошвенной воды приводит к наступлению установившегося режима тем скорее, чем меньше мощность пласта, больше величина вскрытия его скважиной и меньше анизотропия.
Полученные решения могут быть использованы для интерпретации результатов исследования скважин, расчета средневзвешенного давления, расчета предельных безводных дебитов скважин. Ил. 2. С.К.Сохошко, А.П.Телков. 05.09.1988.
УДК. 620.193/. 197
ПОДБОР N - И S - СОДЕРЖАЩИХ ИНГИБИТОРОВ СЕРОВОДОРОДНОЙ КОРРОЗИИ СТАЖ ПУТЕМ СНЯТИЯ ПОЛЯРИЗАЦИОННЫХ КРИВЫХ Алиев Ф.Ю., Джафаров З.И., Курбанов К.В., Юсибов 10.А., Бердяева Н.Р., Абдуллаева Н.Г., Юсибов Ч.А., Лобашев М.Н. (Аз.СХИ им. С.А.Агамалиоглы). Рукопись статьи. 4 с.
ИНГИБИТОР КОРРОЗИЯ СТАЛЬ ПЕРЕМЕШИВАНИЕ СМЕСЬ
Цель работы заключается в исследовании влияния органических веществ на скорость коррозии стали в двухфазной агрессивной среде, состоящей из 3$-ного раствора хлористого натрия и бензина марки Б-70 (в соотношении 1:1). Эта система насыщается сероводородом до концентрации 850 мг/л в расчете на водную фазу. Концентрация сероводорода определяется йодометрическим титрованием.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.