Теория укрупненной скважины Ван Эвердингена и Херста
При исследовании проявления водонапорного режима газовая залежь часто аппроксимируется укрупненной скважиной. На теории укрупненной скважины основаны методики прогнозирования показателей разработки при водонапорном режиме. Кроме того, на ее основе предложены методики уточнения параметров водоносного пласта.
Допустим, укрупненная скважина радиусом Rз дренирует однородный по коллекторским свойствам водоносный пласт с постоянным во времени дебитом воды qB. Согласно решению Ван Эвердингена и Херста, изменение во времени давления Р(Rз) на стенке укрупненной скважины определяется по следующему уравнению:
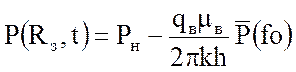 , (34)
, (34)
здесь 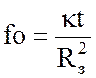 , h, k и
, h, k и ![]() –
толщина и коэффициенты проницаемости и пьезопроводности водоносного пласта
соответственно;
–
толщина и коэффициенты проницаемости и пьезопроводности водоносного пласта
соответственно;
μв – коэффициент динамической вязкости воды;
![]() – табулированная
функция параметра Фурье
– табулированная
функция параметра Фурье ![]() .
.
Пусть укрупненная скважина эксплуатируется с постоянным во времени противодавлением ΔP = Pн - P(R3) на водоносный пласт. Для вычисления суммарного количества воды QB, которое поступит в залежь к моменту t, Ван Эвердингеном и Херстом получено выражение
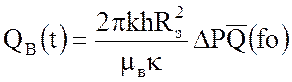 , (35)
, (35)
где ![]() –
табулированная функция параметра Фурье
–
табулированная функция параметра Фурье ![]() .
.
Таблицы функций ![]() и
и
![]() составлены
для случаев бесконечного по протяженности, конечного замкнутого и открытого
водоносного пласта.
составлены
для случаев бесконечного по протяженности, конечного замкнутого и открытого
водоносного пласта.
В качестве бесконечного водоносный пласт может рассматриваться при условии Rк/R3 ≥20, где Rк – радиус внешней границы пласта.
Теория укрупненной скважины наиболее актуальна для газовых и для газоконденсатных месторождений, так как газовые месторождения разрабатываются в режиме истощения пластовой энергии, а большинство газоконденсатных месторождений также разрабатывается без поддержания пластового давления и рано или поздно они переходят на режим истощения пластовой энергии. В результате между водонапорным бассейном и залежью газа происходит увеличение разницы давлений, что вызывает приток воды в залежь газа (укрупненную скважину).
Решения (34) и (35), полученные для случаев qB=const и ΔP = const, и используются, благодаря принципу суперпозиции, для переменных во времени граничных условий на стенке укрупненной скважины.
Приближенная теория укрупненной скважины
С использованием метода интегральных соотношений получено решение для случая эксплуатации укрупненной скважины при переменном во времени дебите воды в виде системы уравнений, в которую входит уравнение материального баланса (33), уравнение притока воды к «укрупненной» скважине (36), уравнение допустимого технологического режима эксплуатации «средней» скважины (26), уравнение притока газа к «средней» скважине (27), уравнение связи потребного числа газовых скважин, отбора газа из месторождения Qи дебита газовой скважины (28).
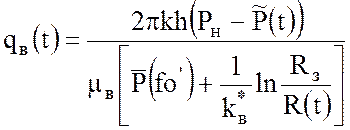 (36)
(36)
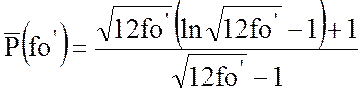 (37)
(37)
![]()
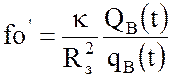 (38)
(38)
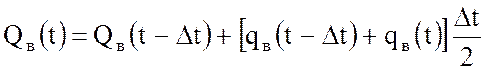 (39)
(39)
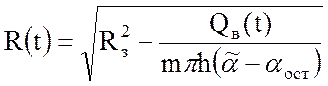 (40)
(40)
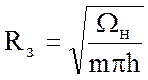 (41)
(41)
С целью единообразия расчетных операций для всех периодов добычи газа остановимся на определении показателей разработки в период падающей добычи с использованием метода последовательных приближений по добытому количеству газа. Пусть на момент t-Δt периода падающей добычи газа все показатели процесса поступления в залежь контурной или подошвенной воды известны. Тогда в первом приближении добытое количество газа из залежи ко времени t оцениваем по формуле
![]() . (42)
. (42)
Это позволяет оценить показатели разработки на момент времени t периода падающей добычи (с учетом обводнения скважин). Во втором и последующих приближениях добытое количество газа из залежи ко времени t уточняется по формуле
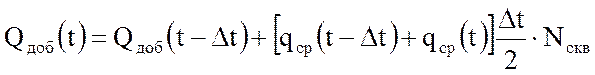 . (43)
. (43)
При этом последовательные приближения проводятся в пределах рассматриваемого интервала времени периода падающей добычи [8].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.