Снижение аварийности забойных скребковых конвейеров, страница 9

Такие направленные на растяжение цепи динами­ческие удары действуют на замкнутый контур цепи (систему цепи) каждый период зацепления зубца звёздочки с цепью. Эти динамические удары являются внешними возмущающими по отношению к системе цепи. Так как реальная тяговая цепь представляет упругое тело с конечной жёсткостью и равномерно распределённой массой, то в ней под дейст­вием динамических ударов возникают продольные деформации (упругое смещение сечений цепи), распространяющиеся по ветвям замкнутого контура цепи в виде упругих волн деформации с определёнными скоростями. После приложения возмущения, возникшая упругая волна растя­жения распространяется от точки набегания цепи на ведущую звёздоч­ку (место приложения динамического удара и начальная граница коле­бательного контура) вдоль грузовой ветви. Дойдя до концевой голов­ки упругая волна преломляется, и далее двигается по порожняковой ветви к приводу. Дойдя до точки сбегания цепи с ведущей звёздочки (конечная граница колебательного контура) упругая волна отражается и следует в обратном направлении к начальной границе контура. Дос­тигнув начальной границы упругая волна отражается и снова соверша­ет пробег в границах контура. Этот процесс повторяется до полного затухания колебательного процесса цепи. Период времени равный пер­вому двукратному пробегу упругой волны по ветвям контура цепи на­зывают периодом основного тона собственных колебаний цепи. Его значение определяют по формуле

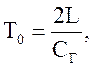                                                   (5.31)

где C_Г и C_П - соответственно скорости распространения упругой      волны на грузовой и порожней ветвях, (м/с); L - длина конвейера (м).

Динамические нагрузки в цепи достигают своего наибольшего значения при резонансе, когда период собственных колебаний цепи (T) равен или кратен периоду внешнего возмущения 2τ (периоду вынужденных колебаний) т.е. если

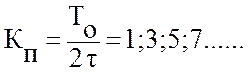                                    (5.32)

Так, например, условие возникновения резонанса с  основным тоном собственных колебаний (К_П = 1) записывается следующим образом

                                                                                                          (5.33)

Период неравномерности хода цепи представляет собой период внешнего возмущения и равен периоду зацепления одного зубца звёз­дочки

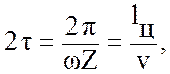с                                            (5.34)

где ω - угловая скорость вращения звёздочки рад/с       (с^-1);

 Z - число зубцов ведущей звёздочки;

l_Ц - величина шага цепи (м);

v - скорость (средняя) движения цепи (м/с). Из равенства (5.34)

В общем случае может быть определены критические скорость движения цепи, числа зубцов приводной звёздочки, величина шага цепи.

Решая совместно уравнения (5.31, 5.32, 5.34) относительно L_кр по­лучаем

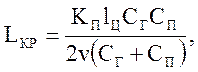                                                                                             (5.35)

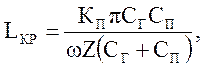                                                                                             (5.36)

где L_КР - критическая длина скребкового конвейера при которой

возможен резонанс (м).

Исследования показывают, что если

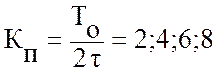                                                                                               (5.37)

то возникает явление, обратное резонансу. При этом собственные и вынужденные колебания совершаются антифазно и династические наг­рузки достигают минимального значения.

Скорости распространения вдоль цепи упругой волны определя­ются для грузовой ветви по формуле

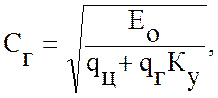                                                                                                (5.38)

для порожняковой ветви по формуле

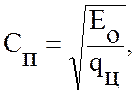                                                                                                      (5.39)

В этих формулах приняты следующие обозначения: E_o - про­дольная жесткость цепи, значения которой приведены в таблице 5.2;

K_У - коэффициент участия движущейся массы груза с тяговой цепью ( К_У = 0,3 - 0,5).

Таблица 5.2

Жёсткость цепей