Снижение аварийности забойных скребковых конвейеров, страница 11

В установках с длинной тяговой цепью при большом её натяже­нии и определённом соотношении скорости, длины и шага цепи воз­можно явление резонанса, если период собственных колебаний цепи будет равен или кратен периоду внешнего возмущения. Динамические нагрузки при резонансе достигают наибольшего значения и в некото­рых случаях могут оказаться причиной разрушения тяговой цепи. Поэтому работа транспортных установок в режиме резонанса или бли­зком к нему недопустима [4, с. 59].

Алогично определению L_кр, определяются критические скоро­сть движения цепи, числа зубцов приводной звёздочки, величина ша­га цепи. Явление резонанса может быть ликвидировано изменением одного из указанных параметров в условиях его возникновения.

Резонанс в тяговых цепях внешне проявляется в повышении не­равномерности хода цепи, особенно вдали от приводной станции, что ясно заметно невооружённым глазом [11, с.162].

Величина динамических усилий вызываемых резонансом, для ск­ребковых конвейеров средней производительности лежит в пределах 5000-12000 Н.Так как загрузка конвейера, жёсткость тяговой цепи и другие параметры конвейера практически никогда не бывают абсо­лютно постоянными, то и явление резонанса в тяговых цепях воз­можно крайне редко. При отсутствии резонанса динамические усилия в существующих конвейерах редко превышают 20-25 % статического натяжения цепи [4, с.60 ].

5.3.8 Характерные углы наклона конвейера

"Угол равновесия порожней ветви" получим, приравни­вая нулю сопротивление движению вниз порожняковой ветви, найден­ное из выражения (11). При этом

                                                 (5.40)

"Угол равновесия грузовой ветви" получим, приравни­вая нулю сопротивление движению вниз гружённой ветви, полученное из выражения (12). При этом

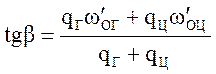                                         (5.41)

"Угол равновесия конвейера" получим, приравнивая ну­лю сумму сопротивлений движению порожняковой и грузовой ветвей из выражений (11) и (12). При этом

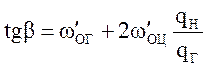                                        (5.42)

При определении "угла равновесия конвейера" по формуле (5.42) не учитываются сопротивления движению цепи на приводных звёздоч­ках, концевых барабанах, на участках изгиба конвейера в плане.

Значение характерных углов конвейера в тяговом расчёте.

"Угол равновесия порожней ветви" является граничным уг­лом, и предопределяет знак для силы сопротивления движению по­рожняковой ветви для рассматриваемых условий.

"Угол равновесия грузовой ветви" предопределяет знак для силы сопротивления дви­жению грузовой ветви конвейера, угол наклона которого больше или меньше угла равновесия.

"Угол равновесия конвейера" является граничным углом, предопределяет знак тягового усилия конвейера, и при угле наклона последнего больше угла равновесия имеет место тормозной режим работы конвейера (приводной электродвигатель ра­ботает в генераторном режиме).

5.3.9 Определение деформации цепи

         Значение сопротивления движению (Н) ветвей цепи определяют по формулам:

     нижней ветви

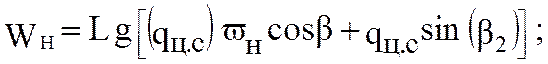                                          (5.43)

     верхней загруженной ветви

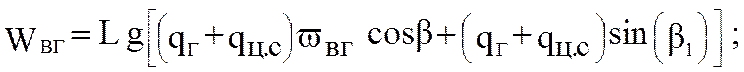    (5.44)

     верхней ветви без груза

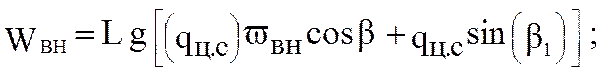                                   (5.45)

     верхней ветви от груза

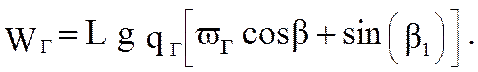                                         (5.46)

Удельную силу сопротивления ветвей ленты определяют по формулам:

                                 = W_H / L;

       = W_ВГ / L;                                                    (5.47)

                                 = W_ВН / L;

                                  = W_Г / L.

     Жёсткость цепи является характеристикой цепи в упругой области. Если жёсткости Е, равной натяжению   S  цепи,   соответствует   значение   относительной   деформации e = 1,  то, следовательно,  определённому  значению  натяжения  S_i  в замкнутом контуре соответствует значение деформации  e_i  =  Dl_i ¤ l_i. Из этого соотношения следует