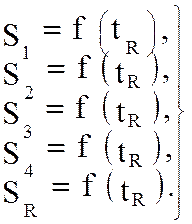Геология \ Подземная разработка пластовых месторождений

Снижение аварийности забойных скребковых конвейеров, страница 13

                                         (5.67)

При рассмотрении  варианта без учета провеса цепи принимаем следующие допущения: цепь рассматривается как стержень с жесткостью Е, и коэффициент сопротивления движению v не зависит от натяжения ленты. При этом принимаем  и уравнения (5.56), (5.58), (5.63), принимают вид 

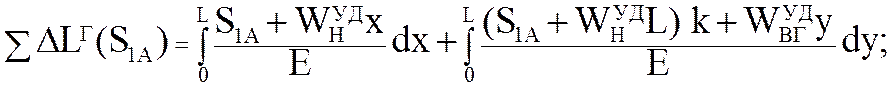 (5.68)

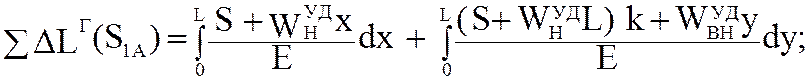             (5.69)

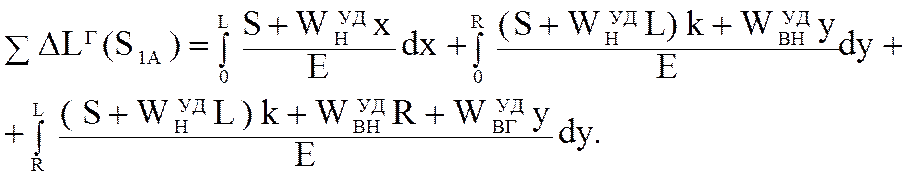(5.70)

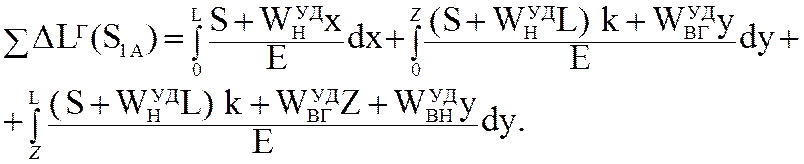             (5.71)

Контрольное значение  определяется суммой деформации замкнутого контура цепи при номинальной загруженности конвейера. Проинтегрировав (5.68), получим

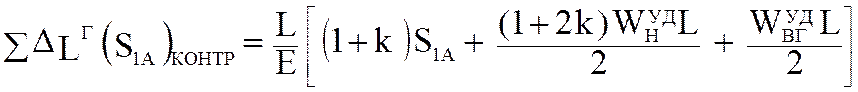      (5.72)

Контрольное значение  S1XX.КОНТР  натяжения ленты в точке 1 определяется при холостом ходе конвейера. Проинтегрировав (5.69), получим

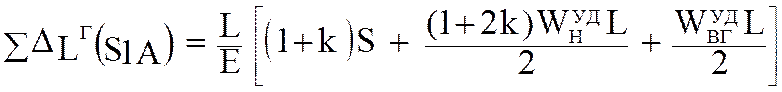
               (5.73)

     Приравняв правые части уравнений (5.72) и (5.73) и  решая полученное равенство относительно  S = S1XX.КОНТР,  получим

     S1XX.КОНТР = S1A  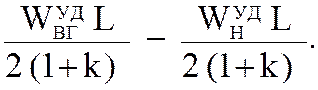+                                (5.74)

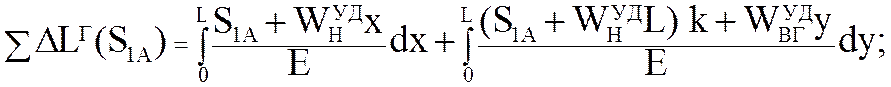 (5.75)

     В формуле (5.68)  первый интеграл определяет деформацию нижней ветви, а второй - деформацию верхней ветви.  Индекс «н» соответствует нижней ветви, а индекс «в» – верхней. ветвей цепи.

     В формуле (5.68) решаем каждый интеграл отдельно. В результате решения уравнения  получили

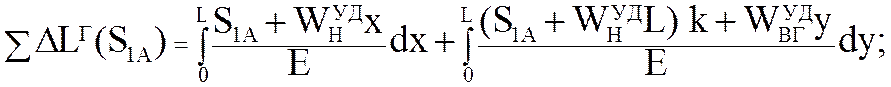 (5.77)

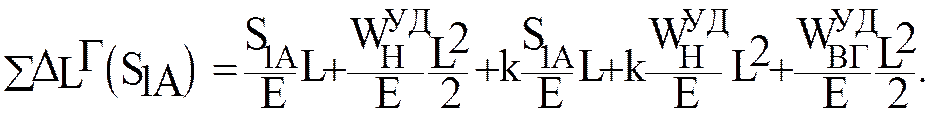
     В  полученном уравнении первые два слагаемых представляют деформацию нижней ветви цепи, а три последующие деформацию верхней ветви цепи. Для проверки суммарную деформацию определяем

 по формуле

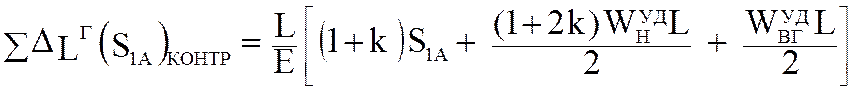      (5.78)

5.3.10 Скорость распространения упругой волны

          Для порожней ветви конвейера

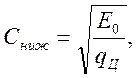                                               (5.79)

          Для загруженной ветви конвейера

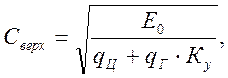                                        (5.80)

          где Ку = 0,3…0,5.

5.4 Исходные данные

     Исходные данные для определения значений деформации ветвей замкнутого контура цепи конвейера:

     1. Длина конвейера – 220 м;

     2. Производительность конвейера – 3000 т/ч;

     3. Скорость движения цепи – 1,28 м/с;

     4. Цепь – двухрядная, центральная  с  межценровым расстоянием равным 150 мм;

     5. Типоразмер цепи – 34 ´ 126;

     6. Жесткость цепи – 6,5×107Н;

     7. Масса цепи со скребками – 105 кг/м;

     8. Угол наклона конвейера – 14 градусов;

     9. Масса груза на одном метре длины конвейера – 651,4 кг/м.

5.5 Определение значений деформации цепи конвейера

5.5.1 Горизонтальный прямолинейный конвейер без груза

Определяем основное сопротивление перемещению цепи порожней и грузовой ветвей:

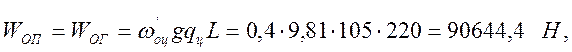
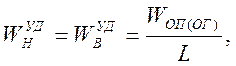
          Деформация верхней и нижней ветвей:

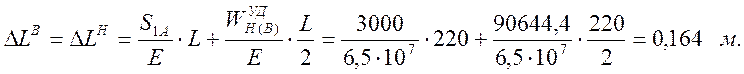
          Скорость распространения упругой волны:

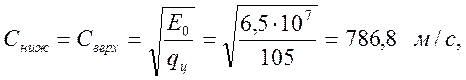
5.5.2 Прямолинейный конвейер, перемещающий груз сверху вниз

          Для порожней ветви:

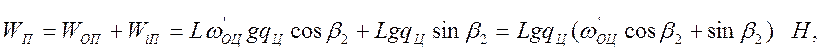
          Для грузовой ветви:

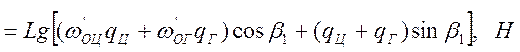
Деформация верхней и нижней ветвей:

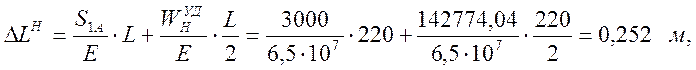
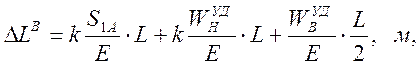
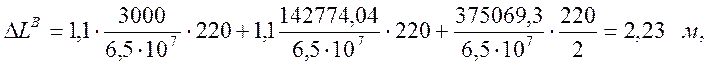
          Скорость распространения упругой волны:

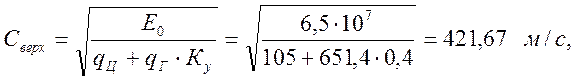
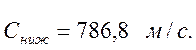
Литература

1. Транспорт на горных предприятиях. Под общей ред. проф. Б.А. Кузнецова. - М.: Недра, 1976 - 552 с.

2. Пухов Ю.С. Транспортные машины. - М.: Недра, 1987. -232с.

3. Шахмейстер Л.Г., Солод Г.И. Подземные конвейерные уста­новки. - М.: Недра, 1976. - 432 с.

4. Григорьев В.Н., Дьяков В.А., Пухов Ю.С. Транспортные ма­шины для подземных разработок. - М.: Недра, 1984. - 383 с.

5. Поляков А. С., Штокман И.Г. Основы теории и расчёты руд­ничных транспортных установок. М.: Госгортехиздат, 1962. -491 с

6. РТЫ 24.076.07. Конвейеры шахтные скребковые передвижны' Тяговый расчет. Методика. Изд. завода "Свет шахтера" - ИГД им. А.А. Скочинского. Харьков, 1972. - 64 с.

7. Штокман И.Г. Динамика тяговых цепей рудничных конвей­еров. - М.: Углетехиздат, 1959. - 288 с.

8. Проектирование и конструирование транспортных машин и комплексов: Учеб. для вузов (Под ред. И.Г. Штокмана. - 2-е изд. перераб. и доп. - М.: Недра, 1986, 392 с.

9. РТМ 12.44. 045-81. Конвейеры шахтные скребковые. Тяговый расчет. - М.: ИГД им. А. А. Скочинского, 1981. - 45 с.

Скачать файл