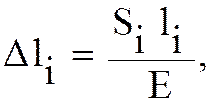(5.48)
где Dli – абсолютная деформация (м) отрезка цепи длиной li (м); Si – натяжение, приложенное к отрезку цепи длиной li (Н).
В общем случае в соответствии с формулой (5.48) абсолютное упругое удлинение в замкнутом контуре цепи на участке нижней ветви от точки x1 до точки x2 можно вычислить следующим образом:
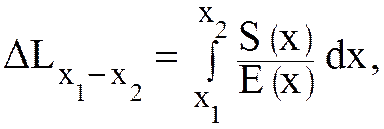(5.49)
где S(x) – натяжение цепи как функция текущей абсциссы x длины цепи; E(x) - жесткость цепи как функция натяжения, определяемого текущей абсциссой x.
Суммарную деформацию цепи при номинальной загруженности и холостом ходе определяют как сумму двух интегралов:
при номинальной загруженности
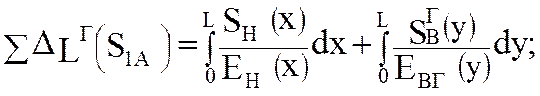(5.50)
при холостом ходе
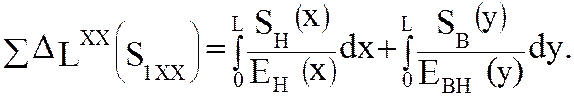(5.51)
В формулах (5.50) и (5.51) первый интеграл определяет деформацию нижней ветви, а второй - деформацию верхней ветви. Индекс «н» соответствует нижней ветви, а индекс «в» – верхней. Жёсткости EH(x), EВГ(y) и ЕВН(у) записаны как функции натяжения соответствующих ветвей цепи.
Натяжение цепи S(x) является линейной функцией абсциссы x, а S(y) - линейной функцией абсциссы y.
При номинальной загруженности конвейера натяжение цепи S(x) и S(y) определяют следующим образом:
на нижней ветви
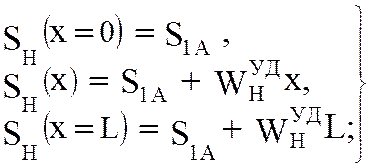(5.52)
на верхней ветви
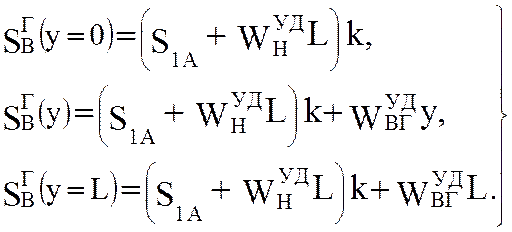(5.53)
При холостом ходе конвейера:
на нижней ветви
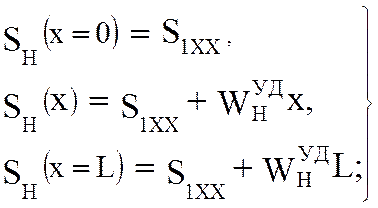(5.54)
для верхней ветви
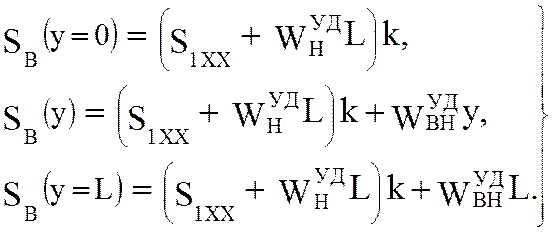(5.55)
Подставив в формулу (5.50) соответствующие значения из формул (5.54), (5.55), получим
.
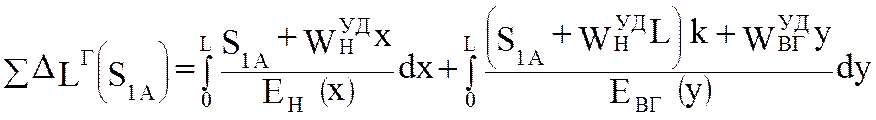(5.56)
Вычисленное по формуле (5.56) значение 
используем в дальнейшем как основу
всех расчетов.
Подставив в формулу (5.51) значения из формул (5.54) и (5.55), получим
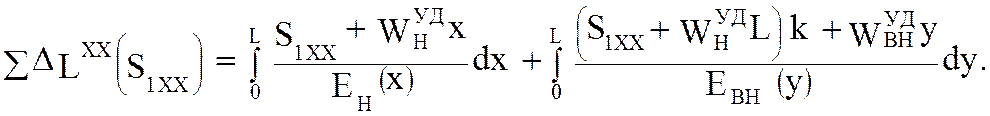
(5.57)
С учётом (5.45) в левой части уравнения (5.57) значение 
заменяем SDL(S1A). При этом получим
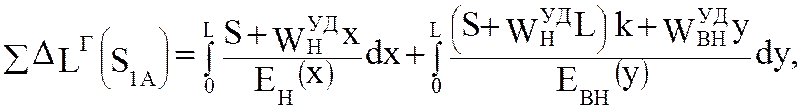(5.58)
где S – искомое значение натяжения ленты в точке 1 (S1ХХ).
Из уравнения (5.58) определяем значение S1XX по известному значению 
В формулах (5.56), (5.57), (5.58) приняты следующие обозначения:
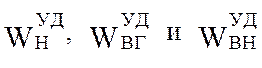– удельные силы сопротивления
движению цепи (Н ¤ м) соответственно на нижней ветви, загруженной и незагруженной верхней
цепи, определяемые при выполнении тягового расчёта конвейера; k – коэффициент, учитывающий
увеличение натяжения цепи за счет действия сил сопротивления движению на
концевом барабане.
При разгрузке конвейера граница раздела плотностей сред верхней ветви (точка r) движется со скоростью движения цепи V, и сумма упругих деформаций складывается из деформаций цепи на трёх участках: нижней ветви; разгруженного и неразгруженного участков верхней ветви. Для определения суммы деформаций надо произвести интегрирование для каждого участка.
В общем случае сумма упругих деформаций
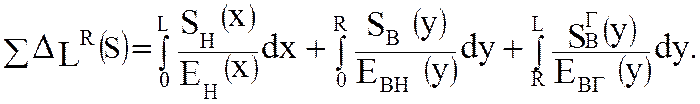(5.59)
Первый интеграл (5.59) определяет деформацию нижней ветви цепи (м), второй - деформацию незагруженного участка верхней ветви, а третий - загруженного участка.
Натяжение цепи SH(x), SB(y) и 
выражают как функцию соответствующих
абсцисс:
на нижней ветви
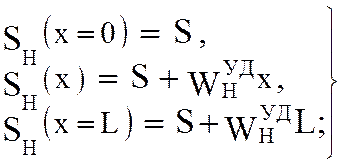(5.60)
на незагруженной части верхней ветви
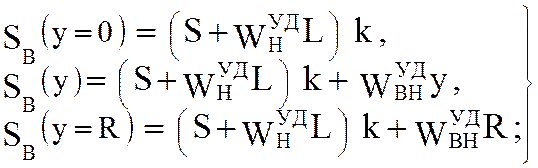(5.61)
на загруженной части верхней ветви
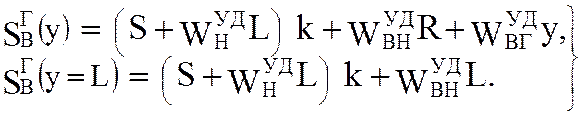(5.62)
Подставив в формулу (5.59) соответствующие значения из (5.60), (5.61) и (5.62), получим
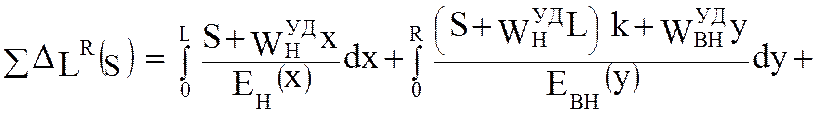
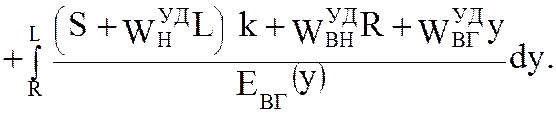(5.63)
С учётом (5.45) в левой части уравнения (5.63) значение 
заменяем 
При этом получаем
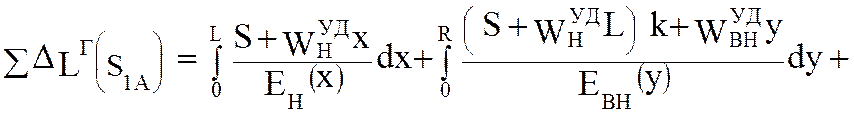
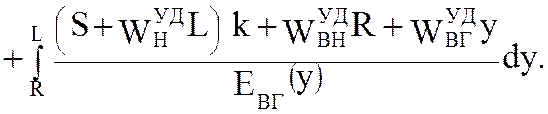(5.64)
Решаем уравнение (5.64) относительно неизвестной величины S для каждого равновесного состояния, определяемого значением R = V t, и определяем значение натяжения ленты в характерных точках замкнутого контура:
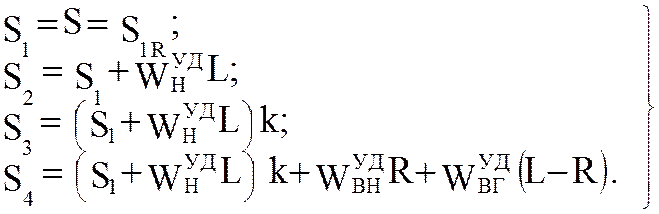(5.65)
(5.66)
По полученным для каждого равновесного состояния значениям S1, S2, S3, S4 и SR можно строить соответствующие графики изменения натяжения цепи в характерных точках в функции времени разгрузки tR, от tR = 0 до tR = L/V через мерный интервал времени (шаг Н):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.