Силовой расчёт рычажного механизма. Синтез зубчатого механизма. Синтез кулачкового механизма

1 СИЛОВОЙ РАСЧЁТ РЫЧАЖНОГО МЕХАНИЗМА

1.1 План скоростей и ускорений

Изобразим схему механизма в положении, для которого требуется сделать силовой расчёт (чертежи, лист 1). В этом положении угол . Построим для этого положения нормальный, не повёрнутый, план скоростей.

Вычислим угловую скорость кривошипа:

.

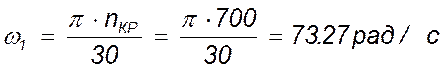Строим план скоростей для группы 2, 3. Построение ведём по следующему векторному уравнению: . При этом скорость  и направленная перпендикулярно линии АВ в сторону, соответствующую направлению угловой скорости звена АВ.  - скорость точки С при вращении звена ВС вокруг оси шарнира В, направленная перпендикулярно линии ВС. Пусть , тогда масштабный коэффициент плана скоростей .

Построение плана скоростей ведём в такой последовательности. Строим решение векторного уравнения, указанного выше: от полюса Р откладываем отрезок pb, изображающий скорость точки В, перпендикулярно линии АВ и в соответствии с направлением вращения звена АВ. Из точки b проводим направление скорости  - линию, перпендикулярную ВС. Переходим к построению направления скорости точки С. Для этого из полюса P проводим линию, параллельную Ay, до пересечения с линией, проведённой перпендикулярно ВС, и получаем точку с – конец вектора скорости точки С. Скорость точки  находим по правилу подобия: конец вектора этой скорости должен лежать на линии bc и делить отрезок bc в том же отношении, в каком точка  делит отрезок , т.е. 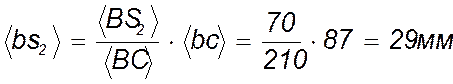. Помещаем в полюс точку a и на этом заканчиваем построение плана скоростей группы 2, 3.

Аналогично поступаем с группой 4, 5.

В результате получаем план скоростей всего механизма.

По формуле  вычислим скорости, необходимые для построения плана ускорений: ; ; ; ; ; .

Определим также угловые скорости звеньев 2 и 4:

.

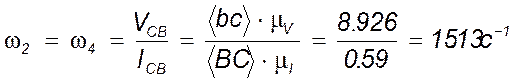Судя по скоростям  и , угловая скорость звена 2 направлена по ходу часовой стрелки, а угловая скорость звена 4 – против хода часовой стрелки.

Определение ускорений.

Строим план ускорений для группы 2, 3. Этот план строится по следующему векторному уравнению:

.

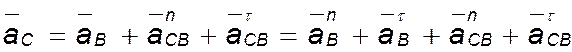Скорость кривошипа при силовом расчёте принята постоянной. При этом ускорение точки В имеет только нормальную составляющую:  и направлено параллельно линии АВ от точки В к точке А, .  - нормальное ускорение точки С во вращательном движении звена ВС относительно точки В, по модулю равное 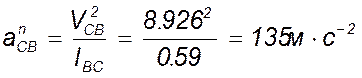 и направленное параллельно линии ВС от точки С к точке В;  - касательное ускорение точки С в том же движении звена ВС, направленное перпендикулярно линии ВС.

Построение плана ускорений ведём в такой последовательности. Строим решение векторного уравнения, указанного выше, для чего от полюса плана qоткладываем отрезок qb, изображающий ускорение , параллельно линии АВ. Пусть , тогда масштабный коэффициент . Далее от точки b откладываем отрезок , изображающий ускорение . По формуле  определим масштабное значение ускорения : . Через точку  проводим направление ускорения  - линию, перпендикулярную линии ВС. Переходим к построению направления ускорения точки C. Для этого из полюса qпроводим линию, параллельную Ay. Точка пересечения её с линией, проведённой перпендикулярно ВС, даёт точку с – конец вектора ускорения точки С. Соединяем точки c и b и получаем вектор полного ускорения точки С при вращении звена ВС относительно точки В, т.е. . Конец вектора ускорения точки  определим по теореме подобия: 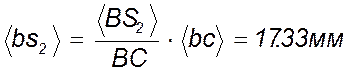. В полюс qпомещаем точку а и на этом заканчиваем построение плана ускорений группы 2, 3.

Аналогично поступаем с группой 4, 5.

В результате получаем план ускорений всего механизма.

По формуле  вычислим ускорения, необходимые для определения сил инерции. Результаты приведены ниже.

; ; ;

; ; .

Вычислим угловые ускорения звеньев 2 и 4:

.

Переносом векторов  и  в точки С и Е соответственно находим, что угловое ускорение звена 2 направлено против хода часовой стрелки, угловое ускорение звена 4 – по ходу часовой стрелки.

1.2 Силы инерции

Модули главного вектора и главного момента сил инерции какого-либо звена определяются по формулам: ; .

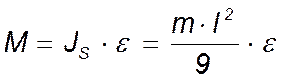Производя вычисления, получим следующие результаты.

 .

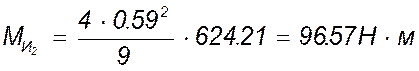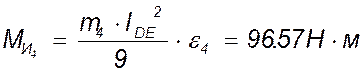 , т.к. звено движется поступательно.

 .

 , т.к. звено движется поступательно.

 , т.к. равны нулю соответствующие ускорения.

1.3 Группы Ассура

Кривошип является звеном с незаданной внешней силой, поэтому принимаем его за начальное звено. При этом первую группу Ассура образует цепь 2,3, вторую – 4,5. Силовой расчёт производится, начиная с последней группы.

1.4 Расчёт группы 4, 5.

Звено 4 находится в равновесии под действием только двух сил  и . При этом, как известно из теоретической механики, они действуют по одной прямой, направлены в противоположные стороны и равны по величине. Реакция  является внутренней силой группы, поэтому на схеме группы эту реакцию не показываем. Реакция  принадлежит вращательной паре D, поэтому разложим её на две составляющих: , направленную перпендикулярно линии DE, и , направленную параллельно линии DE.

Определим силу :

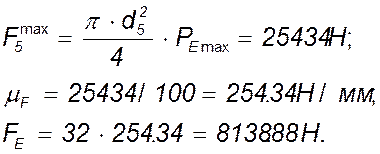
Из равновесия звена 4 получим уравнение моментов относительно точки Е . Отсюда:

Из равновесия группы 4, 5 следует, что . Графическое решение этого уравнения (план сил) даёт:  

1.5 Расчёт группы 2, 3

Звено 2 находится в равновесии под действием только двух сил  и , следовательно, они равны друг другу и взаимно противоположны. Реакция  является внутренней силой группы, поэтому на схеме группы эту реакцию не показываем. Реакция  принадлежит вращательной паре D, поэтому разложим её на две составляющих: , направленную перпендикулярно линии BC, и , направленную параллельно линии BC.