Силовой расчёт рычажного механизма. Синтез зубчатого механизма. Синтез кулачкового механизма, страница 3

Коэффициент перекрытия

.

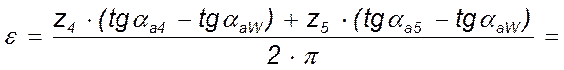
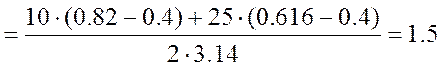2.4. Вычерчивание зацепления 4, 5

Высота зуба колёс 4, 5 . На чертеже зуб должен иметь высоту не менее 40 мм. Требуемое увеличение составляет 40/9.5=4.2. На этом основании принимаем масштаб М4.5:1. Зацепление вычерчиваем в следующем порядке. Отмечаем центры колёс. Проводим основные окружности. По касательной к этим окружностям проводим линию зацепления.

Отмечаем полюс зацепления. Проводим окружности вершин. Строим две эвольвенты, соприкасающиеся, например, в полюсе.

Проводим делительные окружности. Откладываем толщины зубьев по этим окружностям. Находим оси симметрии зубьев и строим противоположные стороны этих зубьев. Проводим окружности впадин. В основаниях зубьев делаем скругления радиусом 0.3 модуля. Это примерно равно радиусу скругления производящей рейки.

Через полюс проводим начальные окружности. Отмечаем границы всей линии зацепления и её активной части. Находим границы активных профилей зубьев.

Определяем коэффициент перекрытия по чертежу:

.

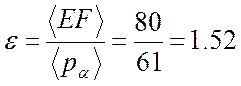С точностью до десятых он совпадает с расчётным коэффициентом – 1.19. Это свидетельствует о правильности синтеза зацепления.     

                                 3 СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА

3.1 Кинематические диаграммы толкателя

Согласно заданию, на фазе подъёма экстремальные значения аналога ускорения толкателя находятся в отношении . Пусть отрезок  равен 80 мм (чертежи, лист 3). Тогда, указанное выше отношение, получим  мм.

          Примем отрезок  равным 100 мм. Чтобы в конце фазы подъема аналог ускорения обратился в ноль, выровняем площади под его положительными и отрицательными ординатами. Для этого поделим отрезок  на части  и , обратно пропорциональные значениям  и . Учитывая, что  мм, получим  мм, откуда  мм. По принятым и вычисленным длинам отрезков построим график аналога ускорения .

          Графики  и  получим двукратным графическим интегрированием аналога ускорения. При первом интегрировании проведём горизонтальные выносные линии от каждой ступени этого аналога. На расстоянии  мм отметим полюс . Из полюса проведём лучи к каждой выноске. Параллельно лучам проведём соответствующие линии графика .

          При повторном интегрировании полюсное расстояние  примем одинаковым с . График  заменим ступенчатой линией. Высоту ступеней выберем так, чтобы треугольники, лежащие выше и ниже этих ступеней (см. интервал 1, 2), были одинаковыми по площади. От каждой ступени проведём горизонтальные выносные линии до упора в координатную ось. Из полюса  проведём лучи к каждой выносной линии. Из начала координат  выстроим цепочку хорд, каждая из которых параллельна своему лучу. Точки излома цепочки хорд дадут искомые ординаты графика .

          Вычислим масштабные коэффициенты по осям построенных графиков. Начнём с графика . По заданию  м; в результате интегрирования отрезок  получился равным 82 мм. Отсюда  м/мм.

          По заданию ; на чертеже этому углу соответствует отрезок  мм.

На этом основании:

 град/мм или 0,011 рад/мм.

          Масштабные коэффициенты по осям  и  определим по формулам [1, с 13]:

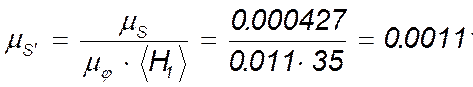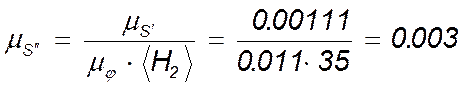 м/мм;

 м/мм.

3.2 Начальный радиус кулачка

Для определения начального радиуса  и эксцентриситета е по диаграммам  и  построим объединённую диаграмму . Все точки диаграммы пронумеруем. При вращении кулачка в направлении, указанном (против хода часовой стрелки), ось  направим влево. Масштабы по осям диаграммы  принимаем одинаковыми и равными некоторому единому значению . Это значение примем так, чтобы отрезок , изображающий  в масштабе , был длиной 50 мм. На этом основании:

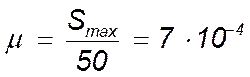 м/мм.

          При переходе от исходных кинематических диаграмм к объединённой диаграмме масштабные пересчёты производят по формулам: