Аналогично определим силу ![]() :
: ![]() .
.
Из равновесия звена 2 получим уравнение
моментов относительно точки C: ![]() . Отсюда:
. Отсюда: ![]()
Из равновесия группы 2, 3 следует, что ![]() . Графическое решение этого уравнения
(план сил) даёт:
. Графическое решение этого уравнения
(план сил) даёт: ![]()
![]()
1.6 Расчёт начального звена (кривошипа 1)
Из равновесия звена 1 следует, что
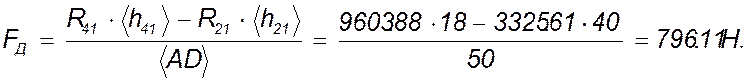
Из
плана сил, построенного по уравнению: ![]() ,
найдём
,
найдём ![]() :
: ![]()
1.7 Проверка силового расчёта
Поверку сделаем с помощью рычага Жуковского. Для этого к повернутому плану скоростей приложим внешние силы механизма и силы инерции его звеньев.
Относительно полюса P сумма моментов всех сил, приложенных к рычагу, должна быть равна нулю. Отсюда
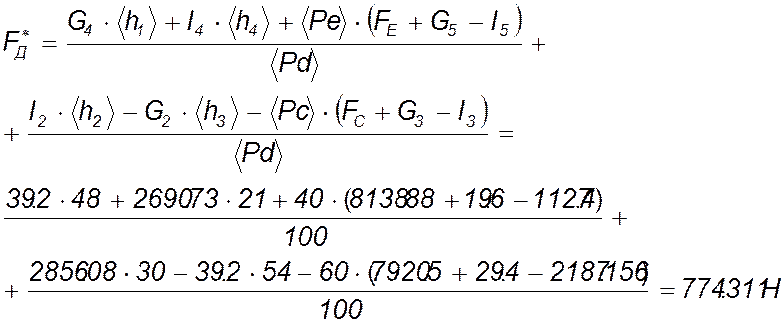
Ошибка силового расчёта
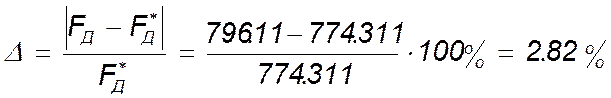 .
.
Для графических расчётов такая ошибка допустима и, следовательно, силовой расчёт сделан правильно.
2 СИНТЕЗ ЗУБЧАТОГО МЕХАНИЗМА
2.1 Подбор чисел зубьев планетарной передачи
Согласно заданию, частота вращения кривошипа равна 365 об/мин, частота вращения электродвигателя – 1425 об/мин. Зная эти величины, определим передаточное отношение от колеса 1 планетарной передачи к кривошипу:
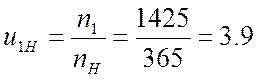 .
.
Согласно (1, с.32), числа зубьев планетарной передачи рассматриваемой схемы находятся в отношении:
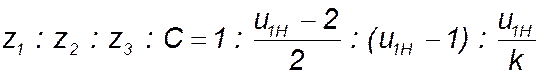 ,
,
где С – любое целое число. После подстановки правая часть данного уравнения последовательно принимает вид:
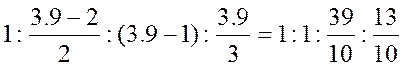 .
.
Чтобы колёса получились с целыми числами зубьев, причём не менее 15…17 (это избавит нас от необходимости делать колёса со смещением), умножим правую часть на 20. После умножения получим:
![]() .
.
Отсюда
![]() ,
, ![]() ,
, ![]() .
.
2.2 Картина линейных и угловых скоростей
Картину линейных скоростей совместим со схемой механизма (чертежи, лист 2). Схему построим по делительным окружностям, т.к. они пропорциональны начальным и, следовательно, картину скоростей не искажают. К тому же в нашем случае начальные и делительные окружности совпадают, т.к. колёса нулевые.
По формуле 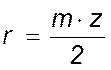 вычислим
радиусы делительных окружностей всех колёс. По заданию модуль m колёс 1…3
равен 2.5. При этом
вычислим
радиусы делительных окружностей всех колёс. По заданию модуль m колёс 1…3
равен 2.5. При этом
![]() ,
, ![]() ,
, ![]() .
.
Схему изобразим в масштабе М1:2, что
соответствует масштабному коэффициенту ![]() .
.
Отложим произвольный отрезок ![]() , изображающий скорость точки А колёс
1 и 2. Точку
, изображающий скорость точки А колёс
1 и 2. Точку ![]() соединим с С – мгновенным
центром вращения колеса 2. Прямая
соединим с С – мгновенным
центром вращения колеса 2. Прямая ![]() является линией
распределения скоростей этого колеса. С помощью
является линией
распределения скоростей этого колеса. С помощью ![]() определим
скорость
определим
скорость ![]() в точке B сателлита и
водила. Соединяя
в точке B сателлита и
водила. Соединяя ![]() и
и ![]() с
О, получим линии распределения скоростей для водила и колеса 1.
с
О, получим линии распределения скоростей для водила и колеса 1.
Построение картины угловых скоростей.
Из точки О произвольного отрезка ОЕ проведём лучи, параллельные линиям
распределения скоростей. Лучи отсекают на горизонтальной прямой отрезки Е1, Е2,
ЕН, пропорциональные угловым скоростям ![]() ,
, ![]() ,
, ![]() соответственно.
По картине угловых скоростей передаточное отношение
соответственно.
По картине угловых скоростей передаточное отношение
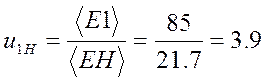 .
.
Это хорошо совпадает с заданным ![]() .
.
2.3. Геометрический расчёт зацепления 4, 5
Исходные данные
Число зубьев колеса 4……………………10
Число зубьев колеса 5……………………25
Модуль,
мм….………….…………………………..![]()
Параметры производящей рейки (ГОСТ 13755 - 81)
Угол профиля,
град…………..……………………![]()
Коэффициент
высоты головки……………..![]()
Коэффициент
радиального зазора……![]()
По блокирующему контуру (1, прил. 3), соответствующему заданным числам зубьев, принимаем:
![]() ;
; ![]() .
.
По выбранным коэффициентам смещения вычисляем инволюту угла зацепления по формуле (1, с. 24):
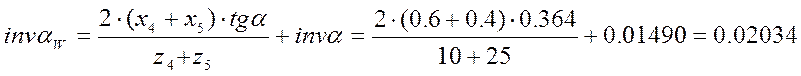 .
.
Отсюда угол
зацепления ![]() .
.
Определив угол зацепления, вычисляем межцентровое расстояние, мм:
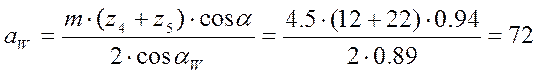 .
.
Радиусы делительных окружностей
![]() ,
,
![]() .
.
Радиусы основных окружностей
![]() ,
,
![]() .
.
Радиусы окружностей впадин
![]() ,
,
![]() .
.
Радиусы окружностей вершин
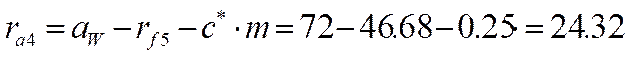 ,
,
![]() .
.
Шаг по делительной окружности
![]() .
.
Толщины зубьев по делительным окружностям
![]() ,
,
![]() .
.
Толщины зубьев по хордам делительных окружностей
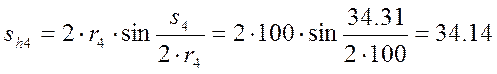 ,
,
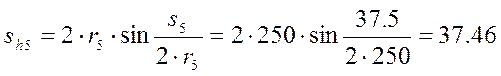 .
.
Углы профиля на окружности вершин
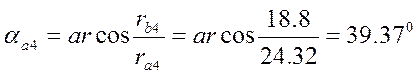 ,
,
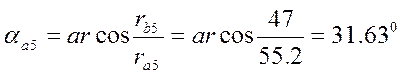 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.