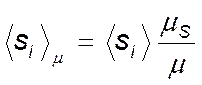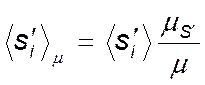Силовой расчёт рычажного механизма. Синтез зубчатого механизма. Синтез кулачкового механизма, страница 4

, ,

где индекс  указывает на отрезки откладываемые в масштабе , т.е. на отрезки, откладываемые на диаграмме .

Так, например, для получения точки 1 следует отложить отрезки 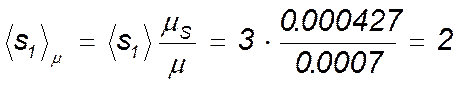мм по оси S и 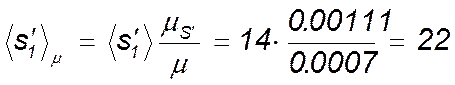мм по оси , на пересечении которых и будет искомая точка. Аналогично получаем все остальные точки объединённой диаграммы .

          По заданию указано только одно значение  допустимого угла давления. Тогда к диаграмме  проводим две касательные под одним и тем же углом  к оси S.

          Выделим штрихами зону, лежащую ниже точки пересечения касательных. Центр кулачка может быть размещён в любой точке заштрихованной зоны. Чтобы начальный радиус кулачка получился наименьшим, поместим этот центр на пересечении этих касательных – в точку А, лежащую при вершине зоны. Расстояние от точки А до начала координат  есть искомый начальный радиус . Эксцентриситет е при этом получается равным нулю.

3.3 Профиль кулачка

          Примем масштаб кулачка М1:2, т.е. в два раза меньше, чем при определении начального радиуса. Из центра А (на чертеже кулачка) радиусом  в соответствии с принятым масштабом проведём начальную окружность НО.

          Через точку А проведём вертикальную прямую , изображающую начальное положение оси толкателя в воображаемом движении этого толкателя относительно неподвижного (при синтезе) кулачка. В сторону, противоположную скорости , откладываем фазовые углы:

, , .

          Углы  и  разбиваем на 8 частей, они разбиты как на кинематических диаграммах..

          Через точки деления начальной окружности проводим радиальные прямые, изображающие все прочие положения оси толкателя в его движении относительно кулачка.

          На каждой из радиальных прямых, в соответствии с выбранным масштабом, откладываем отрезки ,  и им подобные, снятые с оси S диаграммы . В частности, отрезок  равен половине отрезка  диаграммы, а  - половине .

          Точки ,  и им подобные соединяем плавной кривой, которая представляет собой центровой профиль искомого кулачка.

          На выпуклой части центрового профиля находим наиболее изогнутый участок. Этот участок находится между точками  и .

          В окрестности точки, где кривизна профиля кажется наибольшей, проведём две нормали  и . На пересечении нормалей отметим центр кривизны  и замеряем радиус кривизны - мм. Через  и найденное ранее  определяем радиус ролика. Вычислим два значения радиуса ролика:

мм;

мм.

          Выбираем меньшее. Округляя его до целого, получим:

мм.

          Из каждой пронумерованной точки центрового профиля кулачка проводим короткие дуги радиусом ролика . По касательным к этим дугам проводим плавную кривую. Это кривая представляет собой действительный профиль кулачка.

3.4 Углы давления

Из центра А кулачка проведём лучи в каждую пронумерованную точку диаграммы . Например, луч А4 идёт в точку 4. Ожидаемый угол давления , соответствующий этой точке, есть угол наклона луча к оси S. Аналогично определяем ожидаемые углы давления во всех остальных точках.

          По результатам измерений построим график зависимости . Фактические углы давления замерим на кулачке. Сделаем это только для положений 4 и 12, где углы давления экстремальны. Замеры показывают, что фактические углы давления хорошо совпадают с ожидаемыми. Это значит, что задача синтеза решена правильно.

перечень используемой литературы

1. Ермак В.Н. Теория механизмов и машин (курсовое проектирование): Учеб. пособие / В.Н. Ермак, Н.П. Курышкин; ГУ КузГТУ. - Кемерово, 2004.

2. Левитская О.Н. Курс теории механизмов и машин / О.Н. Левитская, Н.И. Левитский. – М.: Высш. шк., 1985.