Матрица переноса 0-й системы координат по Z0 на расстояние S1:
Матрица поворота 0-й с. к. относительно оси X0:
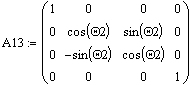
Тогда, перемножив полученные матрицы в порядке A11*A12*A13, получи результирующую матрицу преобразования (А1), связывающую координаты точки в 0-й и 1-й с.к.:
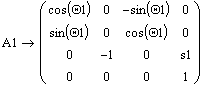
Далее совмещаем 1-ю и 2-ю с.к.
Поворот 1-й системы координат относительно оси Z1:
Переноса 1-й системы координат по Z1 на расстояние S2:
Поворот 1-й системы координат относительно оси X1:
Результирующая матрица преобразования, связывающая координаты точки в 1-й и 2-й с.к.:
A2=A21*A22*A23
Результирующая матрица преобразования, связывающая координаты точки в 2-й и 3-й с.к.:
Тогда для определения положения и ориентации инструмента нужно перемножить результирующие матрицы:
A1* A2*A3=Т
Матрица T имеет вид:
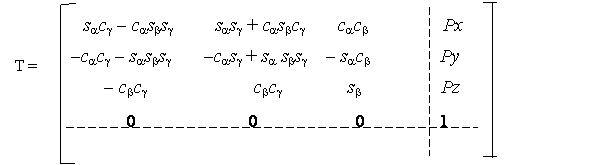
Элементы матриц для 3-х транспортных координат:
x(q)= cos(Q1)*sin(Q3)*S3
y(q)= sin(Q1)*sin(Q3)*S3
z(q)= -cos(Q3)*S3+S1
Матрица Якоби для транспортных координат имеет следующий вид:
Алгоритм ОЗК со встроенным алгоритмом ПЗК:
1) выполним линейное преобразование обобщенных координат:
,
где ki – масштабный коэффициент,
определяющий связь двигателя, датчика положения и ИМ; ai – смещение начала отсчета датчика
положения относительно начала отсчета соответствующей обобщенной координаты
кинематической схемы ИМ; 
-
i-я обобщенная координата, измеренная датчиком положения.
2) Вычисление матрицы Т=А1А2А3
3)
Вычисление координат 
путем подстановки
однородных координат в матрицу Т
4) Проверяем
, если да, то выход
если не, то п. 5
5). Вычисление матрицы В
6).
Проверяем det B < det Bmin, если да, то механизм
остановлен, 
и выход
если нет, то п. 7
7).
Проверяем 
, если да, то 
и к п. 8
если нет, то
и к п. 8
8). Считаем приращение в обобщенных координатах
9).
Проверяем 
, если да, то 
и
к п. 10
иначе к п. 10
10). 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.