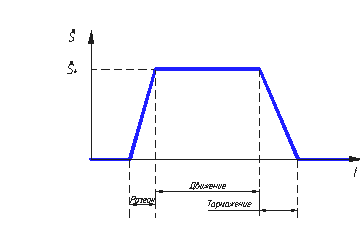
 |
Построения отрезка прямолинейной траектории методом точной КРС (конечно-разностной схемы).
Планирование программной траектории:
Пусть
– вектор начальной точки отрезка
прямой (рис. 2.10); 
– вектор его конечной
точки: 
, 
,v=0,4 – модуль постоянной
контурной скорости, 
– интервал дискретизации.
1)
Выполнить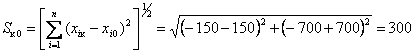 
2)
Если Sк0 > Dс, то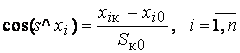 
,иначе
движение отменяется
3) Рассчитывается приращение пути по контуру DS с учетом единиц измерения скорости, положения и времени, определяемых коэффициентом k:
DS = Тvk, где k =0,02
DS = 1.257*10-4
4) Определяются приращения по координатам Dxi:
Dxi = DSсos(S ^ xi), 
.
Dx = DSсos(S ^ x)= 1.257*10-4
Dy = DSсos(S ^ y)=0
Устанавливаем признак разрешения построения программной траектории
Построение программной траектории:
1) Посчитаем проекцию ускорения на соответствующие оси:
2) Если признак разрешения построения установлен, а признак окончания разгона не установлен, то
вычислим скорость на следующем шаге
, где 
-
ускорение разгона по данной координате
вычислим положение на следующем шаге
иначе переходим к п. 4
3) 
,
если да, то установить признак окончания разгона (
-
максимальная скорость)
4) Проверяем пора ли начинать торможение:
определить остаток пути
, если нет, то выход (S-оставшийся путь)
5) установить признак окончания разгона
6)
7) Проверить неравенство
, если да, то снять признак
построения
если нет, то выход
Если признак построения не снят, то на следующем такте все повторяется.
На рисунке 4 представлена кинематическая схема манипулятора, на основании которой мы получили три матрицы преобразований однородных координат.
Рис. 4. Кинематическая схема.
Расчет прямой кинематической задачи для характеристической точки инструмента
( центр инструмента).
Матрица поворота 0-й системы координат относительно оси Z0 имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.