Целенаправленный решатель, страница 12

Решение данной задачи с помощью блок-схемы (см. рис. 10.3) представлено в виде дерева подзадач на рис. 10.2.

Поясним кратко ход решения. По заданному p₁ на шаге Е выбирается метод преобразований, при котором исходный объект s, сравнивается с желаемым s_n (шаг F). Так как с помощью q задача р₁ не решается (в лапах обезьяны нет бананов), то в со­ответствии с этим методом формируется подзадача р₂ — «умень­шить различие D3 в s₁» (шаг I). Поскольку р₂ не труднее супер-задачи p₁ и не имеет вспомогательной задачи, то она и выбира­ется для дальнейшей редукции (шаги I - D).

На шаге Е выбирается метод уменьшения различия, который приводит к выбору подзадачи р₃ — «примепить к s_A оператор f₄». По р_г выбирается метод применения оператора. Так как f₄ не может быть непосредственно применен к s₁ (необходимо, чтобы ящик находился под бананами, а обезьяна — на ящике), то фор­мируется и затем выбирается подзадача р₄ — «уменьшить наи­более трудно устранимое различие D2» (положение ящика). Со­вершенно аналогично формируются и выбираются далее подза­дачи р₅, р₆ и р₇.

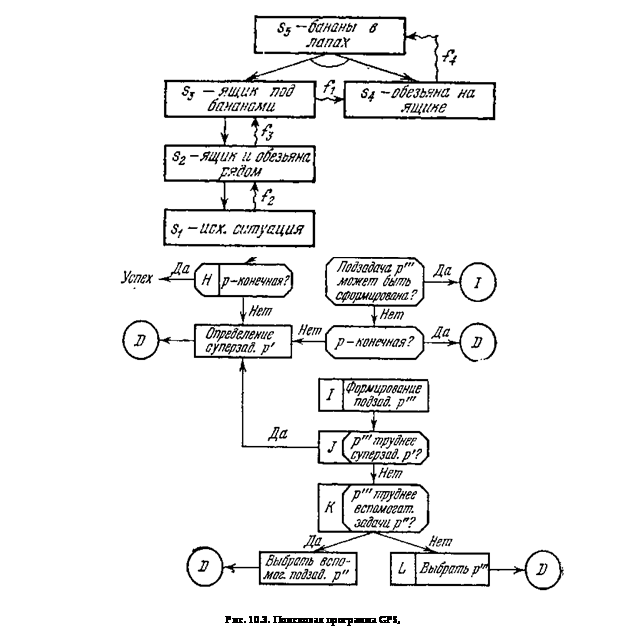
                               Рис. 10.4 Дерево моделей миров s1-s5

На шаге Е для р₇ выбирается метод применения, который ее решает. В итоге формируется объект s₂ (обезьяна и яшик рядом), который играет роль нового исходного состояния, и осуществля­ется переход к суперзадаче p₆. Вновь выбранный метод оказы­вается успешным для решения р₆, поэтому осуществляется пере­ход к суперзадаче р₅. Для р₅ подбирается метод применения при условии, что уже решена подзадача уменьшения различий (от s₁ перешли к s₂). Этот метод приводит к формированию и выбо­ру подзадачи р₈ — «применить к s₂ оператор f₈».

Аналогичным образом формируются и выбираются подзадачи p₉-p₁₃. В итоге формируется план действий f₂ , f_3, f_1, f_4,  кото­рому соответствует последовательность объектов s_1, s₂, s₃, s₄ s₅ = s_n (см. рис. 10.4).