Целенаправленный решатель, страница 11

Всевозможные различия между парами объектов априори упорядочены по степени трудности их устранения и составляют перечень различий. Эти различия могут устраняться только с по­мощью операторов, получаемых путем означивания параметров операторных схем. Процедуральное описание операторных схем включает проверку условий применения оператора и результат его применения, выражаемых в общем случае через переменные. Связь операторов с различиями устанавливается с помощью таблицы связей.

Поиск решений. Система GPS решает три типа задач:
преобразовать объект А в объект B, уменьшить различие D в Аи применить оператор f к объекту А.

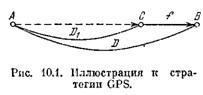
Для нахождения решения GPS применяет обратный поиск, для чего использует эвристику «анализ средств и целей», позво­ляющую сводить задачу к подзадачам, т. е. GPS применяет стра­тегию редукций. Стратегия эта состоит в следующем. Исходная задача (конкретная пара объектов А и В) рассматривается как задача «преобразовать объект А в желаемый объект В». С этой целью GPS выявляет (по упорядоченному списку различий) наи­более трудно устранимое различие D и ставит подзадачу «умень­шить различие D в A»), решение которой состоит в выборе и применении («мысленном» на стадии планирования) подходя­щего оператора f.

Если выбранный оператор f не применяется непосредственно к объекту А, то GPS ставит задачу «применить оператор f к объ­екту A», Решение последней приводит к формированию желае­мого объекта С, к которому может быть применен оператор f Для уменьшения различия D. Теперь возникает задача «преоб­разовать А в С» и т. д. (см. рис. 10.1)..

Рассмотрим схему поиска в GPS. Пусть р — задача, а q — метод ее решения. Пусть также в дереве подзадач р —- родитель­ская вершина, а p` и р"—ее дочерние вершины. Назовем р суперзадачей для p` и p”, а р—вспомогательной задачей для р" (p' решается раньше р"). Так, на рис. 10.2 р₃ представляет собой суперзадачу для р₄ и p₉, а р₄ в свою   очередь   является вспомогательной задачей для р9. Тогда поиск решения в GPS осу­ществляется согласно блок-схеме, приведенной на рис. 10.3.

Пример. Работу каждо­го блока лучше всего пояснить па конкретном примере решения задачи «обезьяна и бананы». Эта задача была предложена профессором Эддинбургского универси­тета Дж. Маккарти в 1963 г. и до сих пор рассматривается как тестовая задача для многих интеллектуальных программ.

Задача состоит в следующем. Обезьяна вместе с ящиком на­ходится в комнате, па потолке   которой   подвешены   бананы.

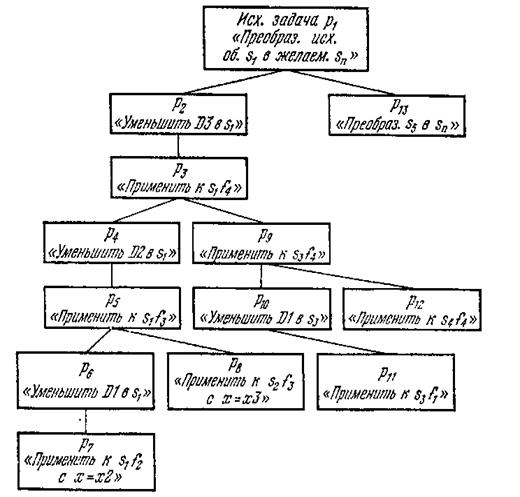Рис. 10.2. Дерево редукций GPS.

Обезьяна может подойти к ящику, передвинуть его и залезть на ящик. Обезьяна может достать бананы только в том случае, если она будет стоять на ящике под бананами. Как это сделать обезьяне?

Проблемная среда.   1) Вспомогательная информация: множество положений на полу X = {x1, х2, x3 — под бананами}.

2) Операторы:

3) Различия: D1 — положение обезьяны, D2 — положение ящика, D3 — содержимое лап обезьяны.

4) Упорядочение различий (по трудности устранения):    D3>D2>D1.

5) Таблица связей: все операторы желательны для уменьше­ния всех различий, т. е. по существу связей нет.

Решение задачи. 1) Исходная задача — «преобразовать исходный объект s₁ в желаемый s_n».

2) Объекты: исходный s₁ — положение обезьяны x1, положе­ние ящика x2, лапы обезьяны пусты; желаемый s_n — бананы у обезьяны в лапах.