Так, результаты опробования оптико-акустического газоанализатора ГИАМ-5М, фиксирующего (в отличие от катарометра ДГРП) содержание в газовоздушной смеси (ГВС) только метана, позволили сделать очень важный практический вывод о том, что в реальных условиях проведения газового каротажа в Западной Сибири аномалии по метану, зафиксированные после выхода из скважины, в дальнейшем не прослеживаются. Таким образом, доказано, что свободный метан полностью дегазируется из ПЖ в
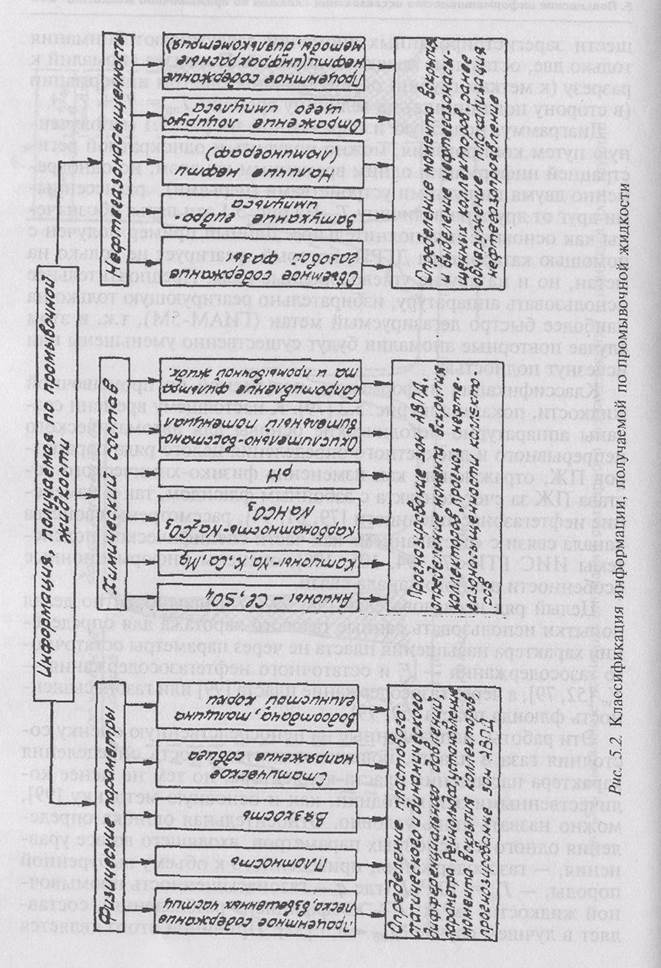
реальных условиях желобной системы, применяемой в Западной Сибири, при движении от устья до насосов. Это обстоятельство имеет принципиальное значение, так как существенно упрощает методику проведения работ из-за ненадобности учета газонасы-шенности ПЖ метаном на входе в скважину [82].
Интересные результаты, объясняющие механизм поведения пластового газа в ПЖ при ее движении к дневной поверхности, получены при опробовании аппаратуры радиоизотопного плотномера ПЖ [167], при поисках новых физических методов прямого определения газонасыщенности ПЖ [52].
Все эти работы и позволили по-новому подойти к проблеме повышения геологической информативности методов исследования скважин по промывочной жидкости.
5.5. Геологическая информативность температуры ПЖ на выходе из скважины
В практике проведения геолого-технологических исследований данные о температуре ПЖ на выходе из скважины используются довольно широко как за рубежом, так и у нас в стране для выделения зон АВПД [49, 81, 169], выделения проницаемых интервалов [81, 182], определения температуры на забое скважины [79, 127]. Однако серьезных теоретических работ, связывающих температуру ПЖ на выходе из скважины с забойными условиями с целью получения обоснования ее геологической информативности, в литературе не встречается.
Э. Е. Лукьяновым совместно с А. И. Филипповым (Башгосу-ниверситет) сделана попытка восполнить этот пробел.
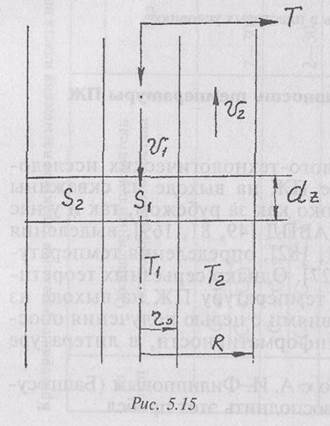
Введем модель, показанную на рис. 5.15, и обозначения:
Г, — температура ПЖ в бурильных трубах, К; Т2 — температура в затрубном пространстве, К;
Дж
С — удельная теплоемкость ПЖ, ———;
К • кг
кг
р — плотность ПЖ, —з~; м
У{ — скорость движения ПЖ в бурильных трубах, м/с;
У2 — скорость движения ПЖ в затрубье, м/с;
/•„ — внутренний радиус бурильных труб, м;
а — коэффициент теплообмена бурильных труб с за-
Вт трубьем, - 2 ;
М ' 14.
^-^ — величина теплового потока в горные породы (из
Вт
горных пород), —2~; м
К — радиус скважины, м.
Предположим, что:
— расход ПЖ в _|>урильных трубах равен расходу ПЖ в затрубье (поглощение или приток в скважину отсутствуют);
— теплообмен по затрубно-му пространству осуществляется по закону Ньютона;
— тепловыделения за счет работы долота на забое пренебрежимо малы;
— частицы выбуриваемых пород (шмала) не изменяют заметно температуру потока.
Составляя уравнение баланса тепловой энергии для потока жидкости в бурильной трубе и затрубном пространстве, приходим к уравнениям:
+а(Г, - Т2)2кг^1с!1 = 0, (5'42)
= 0.
(5'43)
Из (5.42) и (5.43) приходим к уравнениям температуры пото ков жидкости в трубах и затрубном пространстве:
„ с!Т, ,,- с1Т, 2лга ,„, _ , _
О т ——— — '22 ——— "^ ————— \ 2 — 1' "^ —х->— У \*-/ "~
(11 $1 Ср Ср
(5.45)
Далее введем характерные параметры — время бурения т и полную глубину бурения (глубину скважины) Я.
Тогда, складывая (5.44) и (5.45), найдем:
где 0 = У{5} - У252 — расход ПЖ, л/с.
Последнее равенство по сути дела означает, что:
— разность температур не зависит от теплообмена между трубами и затру бьем, а определяется только полным количеством получаемого или отданного тепла;
— разность температур не зависит от соотношения скоростей в трубах и затрубном пространстве.
Последние два вывода положим в основу рассматриваемой теории.
Для поиска решения положим, что Г, и Т2 на забое равны. При этом мы пренебрегаем выделением тепла за счет работы долота.
Тогда из (5.46) получим:
Г2"г'=л-?(г'''№'- (5-47) ••
1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.