Основой для получения производных параметров может стать теория размерности [41, 64, 137, 138].
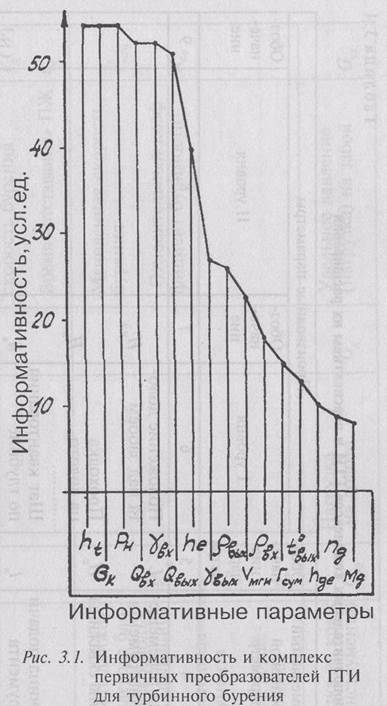
В условиях, когда получены десятки новых параметров ГТИ, имеющих физический смысл, но информационная ценность которых для решения задач ГТИ еще не выяснена, логично не применять методы экспертной оценки или какие-либо другие методы ранжирования ценности информации, как это делалось автором ранее [83], а сделать допущение информационной равнозначности всех основных и производных величин ГТИ.
Из теории информации известно [110], что количество информации, равное разности исходной и оставшейся после измерения энтропии, записывается для случая равномерного закона распределения плотности вероятности как
/ « Н(Х} - Н(Х / X,) = \оё(Х2 -Х})-
-1082А - 108^=^- - -1овТ^1Г, <16>
2Д X 2 — л,
где ЩХ) — энтропия, характеризующая неопределенность измеряемой величины перед измерением (исходная энтропия);
ЩХ/ХП) — энтропия, характеризующая неопределенность, оставшуюся после получения показания прибора (условная энтропия);
Хъ Х2 — начало и конец диапазона измерения;
±Д — абсолютная погрешность измерения.
Единицы измерения как энтропии, так и информации зависят от выбора основания логарифма в приведенном выражении. При использовании десятичных логарифмов единица измерения называется — дит, в случае двоичных логарифмов — бит, а при использовании натуральных логарифмов — нит.
Учитывая, что на данном этапе рассмотрения проблемы, когда отсутствуют сведения как по диапазонам измерения вновь полученных величин, так и по абсолютной погрешности применяемых измерительных средств — Д, применять общепринятые в информационной теории измерительных устройств единицы информации невозможно.
Поэтому на данном этапе введем понятие условной единицы информации (УЕИ), которое применительно к проблеме получения информации при ГТИ может быть сформулировано следующим образом.
Условная единица информации равна количеству информации, получаемому при условии протяженности диапазона измерения х2 ~~ х} в 50 единиц шкалы и абсолютной погрешности измерения Д — 2,5.
Тогда при использовании десятичных логарифмов
УЕИ = ^^~- = 1В 27^ = 1ё1° = 1ДИТ' <3'7>
Сделаем допущение, что как основные, так и производные физические величины обладают информативностью в 1 УЕИ (1 дит), т.е. информативно равнозначны между собой.
Составим таблицу информативности основных параметров ГТИ (табл. 3.6), представляющую собой матрицу измеряемых параметров и производных определяемых параметров. На пересечении определяется количество случаев применения измеряемых параметров для получения производного параметра, взятое из табл. 3.3, 3.4, 3.5.
Например: измеряемый параметр Ь один раз применяется для определения Ь, 1 раз — для определения т, 4 раза — для определения/ 5 раз — для определения К и т.д.
Столбец справа (Т) и нижняя строка (I) матрицы представляют собой сумму случаев применения конкретного измеряемого параметра и сумму случаев применения измеряемых параметров для определения конкретного производного параметра, соответственно.
Общее число параметров (без параметров комплекса 5) составляет 190, общее число случаев применения измеряемых параметров — 476. Следовательно, суммарная информативность параметров 4 комплексов составляет 190 УЕИ, а средняя информативность 1-го измеряемого параметра в производных параметрах
190УЕИ у = 0399 = 04УЕИ
•* спп д^,- и^у? = IV* л-.п.
Исходя из этого, в табл. 3.6 показана информативность каждого измеряемого параметра в группе задач, решаемых 4 измерительными комплексами, а также информативность производных параметров в этой группе задач (строка ниже матрицы).

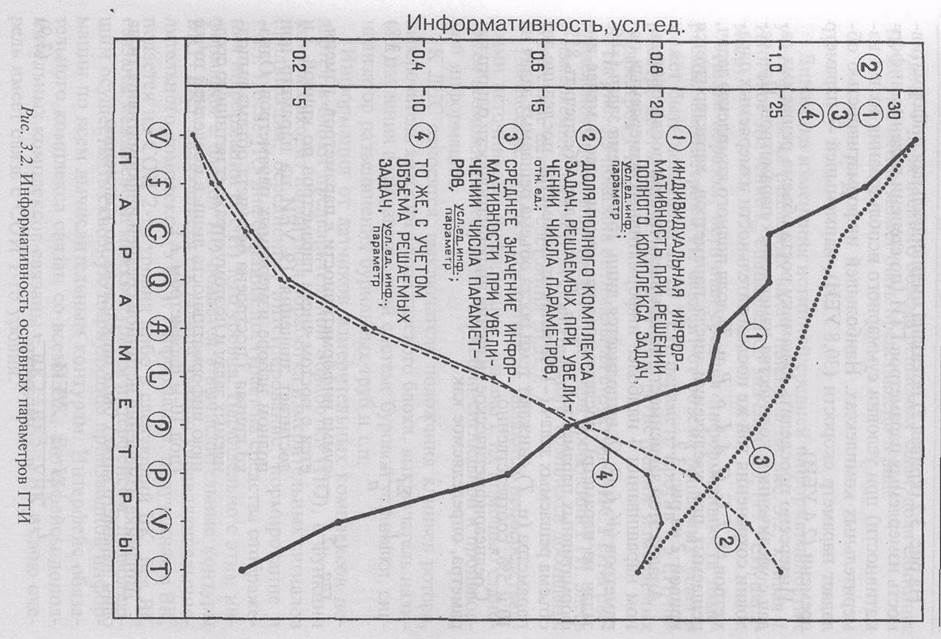
На рис. 3.2 (кривая 7) показана индивидуальная информативность измеряемых параметров ГТИ (по степени падения информативности) при условии суммарного использования их в 4 измерительных комплексах. Наибольшей информативностью обладает параметр скорости (30,8 УЕИ), наименьшей — параметр времени (2,4 УЕИ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.