На рис. 3.4 показана информативность комплексов ГТИ в виде интегральной кривой роста информативности при последовательном наращивании измерительных комплексов и последовательно-параллельной работе вычислительных контуров ВК1-=-ВК5. Суммарная информативность ИИС ГТИ при решении вышеперечисленного объема задач может достигать 200 УЕИ.
3.4. Методы получения комплексных производных параметров, являющихся моделями изучаемого процесса
Полученные с помощью метода размерностей размерные и безразмерные физические величины (комплексные производные параметры) по существу являются математическими моделями составляющих процесса бурения, в силу чего отражают как особенности процесса, так и свойства разбуриваемого разреза.
В табл. 3.3, 3.4, 3.5 показаны наиболее простые по структуре производные параметры. Можно показать целый ряд приемов, позволяющих получить более сложные комплексные производные параметры, а также построить усложняющиеся ряды математических моделей процесса бурения с привлечением различного количества первичной информации.
Сформулируем некоторые правила получения комплексных производных параметров.
1. Прямое перемножение безразмерных величин. Для этой цели строится матрица основных безразмерных величин. Диагональ матрицы дает квадраты основных безразмерных параметров. Симметрично относительно диагонали матрицы получаются результаты перемножения основных безразмерных величин.
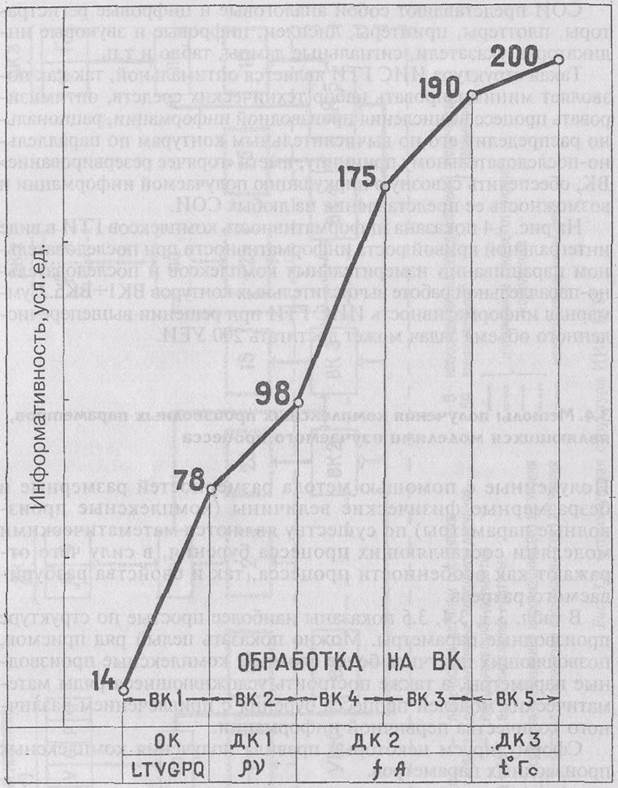
Комплексы ГТИ
Рис. 3.4. Информативность комплексов ГТИ
2. Обратное перемножение безразмерных величин. В этом случае строится матрица основных безразмерных величин и их обратных значений (также безразмерных). По диагонали матрицы получаются значения параметров, численно равные 1, а симметрично относительно диагонали матрицы — результаты перемножения основных безразмерных параметров, имеющих обратное (перевернутое) расположение входящих в формулу членов.
3. Последовательное перемножение нескольких основных безразмерных величин.
4. Последовательное деление нескольких основных безразмерных величин.
5. Получение безразмерных величин из размерных путем деления выражения на величину— основной носитель размерности.
6. Получение безразмерных величин из размерных путем деления выражения на величину — производный носитель размерности.
7. Получение размерных величин путем перемножения основного носителя размерности с безразмерной величиной.
8. Получение размерных величин путем перемножения производного носителя размерности на безразмерную величину.
9. Получение размерных величин по определяющим формулам с использованием основного и производного носителей размерности.
10. Получение размерных величин по определяющим формулам с использованием производных носителей размерностей.
11. Получение безразмерных величин путем отношения величины приращения параметра к величине самого параметра.
Это могут быть отношения приращений к средневзвешенным значениям параметра, отношения значений параметров в любой момент времени к их средневзвешенным значениям и т.п.
12. Получение обобщенных безразмерных комплексов путем перемножения относительных параметров, сгруппированных с учетом их реакции на изменение изучаемого процесса.
Сформулированные на основе теории размерности 12 правил получения производных размерных и безразмерных величин открывают большие возможности определения усложняющихся рядов физических величин, являющихся математическими моделями процесса бурения.
Безусловно, все они не могут быть использованы в процессе ГТИ, так как, во-первых, такое количество информации явно избыточно, а, во-вторых, ИИС ГТИ с любой степенью компьютеризации будут иметь конечные вычислительные возможности, однако из очень большого количества физических величин достаточно просто построить усложняющиеся математические модели, отражающие особенности процесса и свойств горных пород, наиболее подходящие для описания конкретных случаев реального разнообразия горно-геологических и технологических условий бурения глубоких поисково-разведочных и эксплуатационных скважин.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.