Визначення закону надійності невідновлюваних технічних об'єктів

Лабораторна робота №1

Тема: Визначення закону надійності невідновлюваних технічних об'єктів

Мета роботи - опанувати методику кількісно - обґрунтованого визначення закону розподілу  надійності елементів технологічної системи, що працюють до першої відмови.

КОРОТКІ ТЕОРЕТИЧНІ ПОЛОЖЕННЯ

Закони розподілу відмов i їх характеристики.

Закон розподілу відмов – з теорії імовірностей, це неперервний закон розподілу випадкових величин, що описує характер перебігу термінів роботи виробів.

Види законів розподілу:

ü Нормальний – конструктивно досконалі вироби (нормальне зношення);

ü Експоненціальний – не досконала конструкція або технологія;

ü Логарифмічно-нормальний – нормальна робота (старіння);

ü Вейбула – припрацювання;

ü Релея – зношення через зовнішні фактори;

ü Пуассона – зміна терміну роботи в часі, для кількох виробів;

ü Рівноімовірний – зношення під впливом сталого домінуючого фактора;

ü Композиційний – робота в умовах, не передбачених ТУ.

Закон Гауса (нормальний). Область застосування.

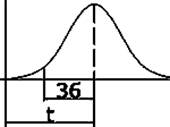Описує термін роботи виробів, що відпрацьовані конструктивно і технологічно, тобто такі, що в процесі експлуатації відмовляють через зношення деталей.

Диференціальна функція (для побудови графіка): 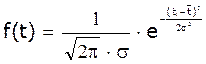, де s - середньоквадратичне відхилення термінів роботи, t – гарантійний термін служби. Чим більше 3s, тим вища якість виробу. Коефіцієнт варіації: v(t) = 0,25...0,45.

Інтегральна функція (інтервал часу для відновлення системи): .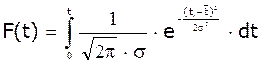

Експоненціальний закон. Область застосування.

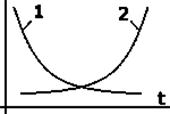Описує термін роботи виробів, конструкція яких не досконала.

Диференціальна функція: , де l - інтенсивність відмов. Інтегральна функція: .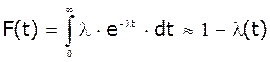

Математичне очікування: 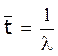, дисперсія: 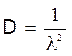, коефіцієнт варіації: v(t) = 1.

Логарифмічно-нормальний закон. Область застосування.

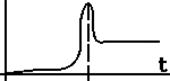Описує термін роботи виробів на стадії нормальної роботи, основна причина відмов – старіння і втомленість.

Диференціальна функція: .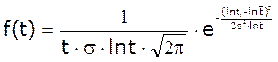

Інтегральна функція: 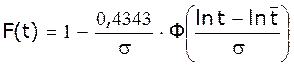, де Ф – табличне значення функції ла Пласа. Математичне очікування: , дисперсія: .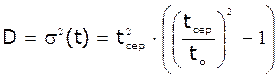

Закон Вейбула. Область застосування.

Описує термін роботи виробів на 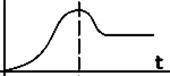стадії припрацювання.

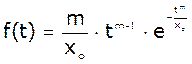Диференціальна функція: , де m і х_о – параметри закону розподілу. Інтегральна функція: .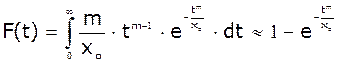

Математичне очікування: 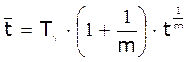, де Т_g - табличне значення g-% функції розподілу термінів роботи. При m®3,3 закон Вейбула подібний закону Гауса, при m®1...2 – закону Релея. І відображає наскільки технологія відповідає конструкції, тобто технологічний рівень виробництва.

Закон Релея.Область застосування.

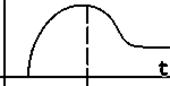Описує термін роботи виробів, коли зношення відбувається під дією зовнішніх факторів.

Диференціальна функція: 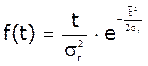, де 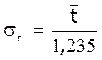 - параметр закону.

Інтегральна функція: .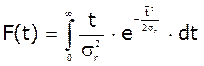

 Вибір закону розподілу.

Вибір закону розподілу здійснюється на основі гістограми, де зображують дані випробувань.

Для розрахунку вибирають ряд, в якому відтворюють інтервали проведення випробувань і кількість відмов для кожного інтервалу. Кількість інтервалів не менше 5 (як правило 5...12). Інтервали можуть біти однаковими і різними, залежно від умов досліджень.

В процесі випробування в ряд заносять значення імовірностей і кількість відмов. На основі ряду розраховують кількісні характеристики: імовірність безвідмовної роботи P(t), математичне очікування M(t), дисперсія D(t), коефіцієнт варіації v(t).

За коефіцієнтом варіації і гістограми приймається гіпотеза про закон щільності розподілу термінів служби.

Статистична перевірка гіпотез про прийняття закону розподілу.

Вибір закону розподілу здійснюється на стадії розрахунку надійності за наявністю статистичних даних. Залежно від гіпотези маємо достовірність, результат, ефективність висновків і рекомендацій.

Здійснюється за критеріями:

ü Мізеса;

ü Пірсона;

ü Колмогорова;

ü Романовського.

Основні критерії узгодження при виборі закону розподілу термінів служби.

Критерій Мізеса: , де N – кількість виробів на випробуванні, z_a - критичне значення критерію, визначається за таблицею, залежно від похибки, a - рівень значимості, що задається при розробці (a = 0,05 – для звичайних технічних систем, a = 0,1 – для відповідальних систем, таких як рульове і гальма).

Критерій Пірсона: , a - рівень значимості, r = k – s – степінь свободи, k – кількість розрядів в таблиці розподілу, s – число констант в законі розподілу.

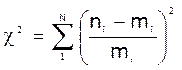, де n_i – кількість випадкових величин в і-му інтервалі, 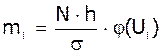 – теоретичні частості випадкових величин в і-му інтервалі, h – ширина інтервалу, , .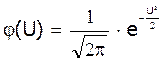

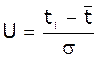Критерій Колмогорова: , де  - найбільше по модулю відхилення теоретичної кривої закону розподілу від експериментальної.

Критерій Романовського: 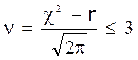, якщо умова справджується, то гіпотеза вірна.

ПРАВИЛА ВИБОРУ ВАРІАНТУ

Правила вибору варіанту – студент обирає варіант виконання завдань  за сумою двох останніх цифр залікової книжки.

Приклад: номер залікової книжки СМХ 024 відповідає (2+4=6) шостому варіанту.