












Корабли совершают плавание по водной поверхности Земли. Поэтому для расчета наивыгоднейшего и безопасного пути корабля необходимо знать форму и размеры Земли. Земля имеет неправильную геометрическую форму, но совпадающую с формой ни одного из известных геометрических тел, и, следовательно, не может быть представлена в виде правильной геометрической фигуры.
Неправильная в математическом отношении фигура, образованная уровенной поверхностью морей и океанов, мысленно продолженной подо все материки, называется геоидом (рис. 1.1).
Поверхность геоида во всех точках перпендикулярна отвесной линии.
Вследствие неправильности формы геоида обработка измерений, относимых к его поверхности, очень сложна. Поэтому при решении основных задач кораблевождения пользуются сходностью геоида с математически правильным телом - эллипсоидом вращения (сфероидом) - фигурой, образованной вращением эллипса вокруг малой оси (рис. 1.2).
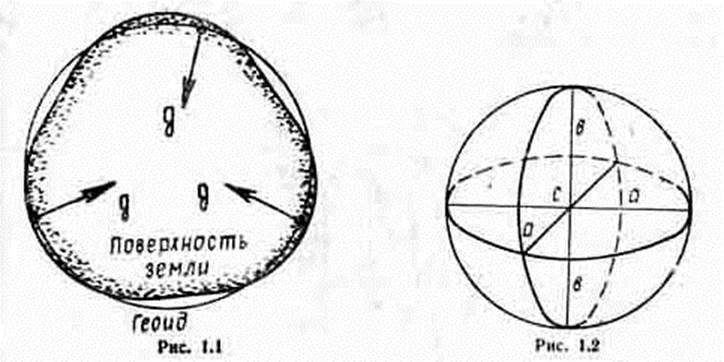
Эллипсоид вращения определенных размеров, принятый за фигуру Земли в данном государстве, называется референц-эллипсоидом.
В Советском Союзе с 1946 г. в качестве референц-эллипсоида принят эллипсоид Ф. Н. Красовского с размерами:
- большая полуось а=6378245 м;
- малая полуось b=6306863 м;
- полярное сжатие (относительная разность полуосей)
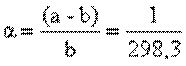
- эксцентриситет
![]()
Референц-эллипсоид Красовского имеет максимальное отклонение от геоида, не превышающее 100-150 м. Этот эллипсоид принят за модель Земли и в ряде других стран (в Польше, Венгрии, Болгарии, Румынии и др.).
При решении большинства задач навигации Землю принимают за шар. Если предположить, что объем Земли-шара равен объему земного сфероида (референц-эллипсоида Красовского), то радиус Земли-шара находится из уравнения
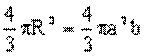
В этом случае R=6371,1 км.
Для ориентирования наблюдателя на земной поверхности используются следующие условные точки, линии и плоскости (рис. 1.3).
Земная ось - воображаемая прямая PNPS, вокруг которой происходит суточное вращение Земли. Эта ось совпадает с малой осью земного эллипсоида.
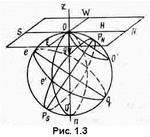
Географические полюса Земли PN и PS - точки пересечения земной оси с поверхностью Земли. Полюс РN, со стороны которого вращение Земли усматривается против движения часовой стрелки, называется Северным, противоположный полюс PS - Южный.
Параллели - линии ОО', образованные пересечением плоскостей, перпендикулярных к земной оси, с поверхностью земного эллипсоида.
Экватор - наибольшая параллель eq, плоскость которой проходит через центр Земли.
Плоскости истинных (географических) меридианов - плоскости, проходящие через земную ось.
Меридиан наблюдателя - меридиан, проходящий через место наблюдателя. Если, например, наблюдатель находится в точке О, то меридианом этого наблюдателя являются линия РNОPSО'.
Вертикальная (или отвесная) линия - прямая ZОn, совпадающая с направлением силы тяжести в данной точке.
Зенит наблюдателя Z и надир n - точки пересечения отвесной линии с воображаемой небесной сферой.
Плоскость истинного горизонта наблюдателя - горизонтальная плоскость Н, проходящая через место наблюдателя перпендикулярно отвесной линии.
Полуденная линия - линия NS, образованная пересечением плоскостью меридиана наблюдателя плоскости истинного горизонта. Направление от О к N называется северной частью истинного меридиана, а направление от О к S - южной частью истинного меридиана.
Плоскости вертикалов, или вертикальные плоскости - плоскости, проходящие через отвесную линию.
Плоскость первого вертикала - вертикальная плоскость Q, перпендикулярная плоскости меридиана наблюдателя. Линия восток-запад ЕW - линия пересечения плоскостью первого вертикала плоскости истинного горизонта наблюдателя. Эта линия соответствует направлениям из места наблюдателя на восток и на запад.
Полуденная линия NS и линия EW являются главными направлениями (румбами).
Относительно указанных точек, линии и плоскостей определяется положение объектов па земной поверхности и задаются направления с одной точки на другую.
К основным направлениям, принятым в кораблевождении, относятся курс, пеленг и курсовой угол.
Истинным курсом корабля (ИК) называется угол в плоскости истинного горизонта между северной частью истинного меридиана и диаметральной плоскостью корабля по направлению его движения (рис. 1.4).
Истинным пеленгом (ИП) называется угол в плоскости истинного горизонта между северной частью истинного меридиана и направлением на объект. Направление, отличающееся от истинного пеленга на 180°, называется обратным истинным пеленгом (ОИП).
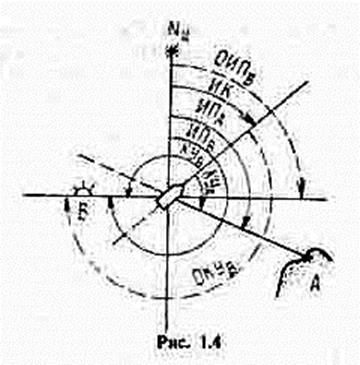
Объектами пеленгования могут быть навигационные ориентиры, корабли, суда и предметы в море, имеющие значение для обеспечения безопасности плавания и боевой деятельности корабля.
Курсовым углом (КУ или q) называется угол в плоскости истинного горизонта между носовой частью диаметральной плоскости корабля (линией курса) и направлением на объект (линией пеленга).
Истинные курсы и пеленги отсчитываются, как правило, в круговой системе отсчета от 0 по ходу часовой стрелки до 360°. По круговой системе градуируются отсчетные шкалы систем курсоуказания, шкалы и лимбы средств зрительного и технического наблюдения, служащие для определения направлений в море. Курсовые углы отсчитываются в полукруговой системе от 0 до 180° с указанием наименования борта. При вычислениях курсовым углам правого борта присваивается знак "плюс", курсовым углам левого борта - знак "минус".
Например, курсовой угол 45° л. б. может быть записан так: КУ = q = - 45°, курсовой угол 110° п.б. - КУ = q = + 110°.
Некоторые средства пеленгования и наблюдения имеют шкалы курсовых углов, отградуированные в круговой системе отсчета (магнитные компасы, перископы, визиры, радиопеленгаторы и т. п.). Началом отсчета является диаметральная плоскость корабля.
Между истинным курсом, истинным пеленгом и курсовым углом существует зависимость, выраженная формулами:
ИП = ИК + КУ; ИК = ИП - КУ; КУ = ИП - ИК. (1.1)
Формулы (1.1) алгебраические. Это значит, что аргументы подставляются со своими знаками. Если в результате расчета ИП или ИК получится со знаком "минус", берется их дополнение до 360° со знаком "плюс". Если КУ получится больше 180°, его нужно вычесть из 360° и изменить направление борта.
Направление на объект, перпендикулярное диаметральной плоскости корабля (КУ=90° левого или правого борта), называется траверзом.
Истинный и обратный истинный пеленги связаны соотношениями:
ИП = ОИП ± 180°; ОИП = ИП ± 180°.
В кораблевождении основными являются географическая и полярная системы координат. Географическая система координат отнесена к земному эллипсоиду.
В географической системе координат положение точки на поверхности Земли определяется широтой и долготой (рис. 1.5).
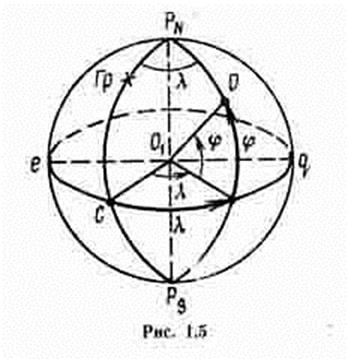
Координатными осями в этой системе являются экватор еСq и начальный меридиан, за который принят меридиан Гринвича (меридиан РNСРS).
Географической широтой j точки называется угол между плоскостью экватора и нормалью к поверхности земного эллипсоида в данной точке. Широта измеряется дугой меридиана от экватора до параллели данной точки. Счет широты ведется в градусах, минутах и десятых долях минуты в пределах от 0 до 90° (от экватора до полюсов). Широтам Северного полушария приписывается наименование North (N) или знак "плюс" (при вычислениях), широтам Южного полушария - наименование South (S) или знак "минус".
Географической долготой l точки называется двугранный угол между плоскостью Гринвичского меридиана и плоскостью меридиана данной точки. Долгота измеряется меньшей дугой экватора от Гринвичского меридиана до меридиана данной точки. Счет долгот ведется в градусах, минутах и десятых долях минуты в пределах от 0 до 180°. Долготам Восточного полушария приписывается наименование East (Е) или знак "плюс", долготам Западного полушария - наименование West (W) или знак "минус".
Пример записи географических координат:
j = 59°46,3'N; l = 28°14,0'W
или
j = +59°46,3'N; l = -28°14,0'W
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.