Процесс кораблевождения связан с измерением на земной поверхности различных углов и направлений, которые затем прокладываются на карте. Это выполняется наиболее просто, если углы, измеренные на местности, равны соответствующим углам на карте. Отсюда второе основное требование к картографической проекции морской навигационной карты: проекция должна быть равноугольной.
Выполнению этого требования в наибольшей степени способствует опознание обстановки на местности и на карте и обусловливает прямоугольность картографической сетки. Действительно, меридианы и параллели пересекаются на земной поверхности под углом 90°, следовательно, при равноугольности проекции под таким же углом они пересекаются и на карте.
Указанным требованиям удовлетворяет прямая равноугольная цилиндрическая проекция, разработанная голландским картографом Герардом Кремером (1512-1594), известным под именем Меркатор.
Для уяснения принципа построения проекции Меркатора (меркаторской проекции) примем Землю за шар и будем рассматривать ее модель - условный глобус. Пусть цилиндр касается условного глобуса по экватору еq (рис. 1.10, а). При этом ось цилиндра совпадает с осью условного глобуса. Меридианы условного глобуса спроектируем на боковую поверхность цилиндра так, чтобы каждая проекция оставалась в плоскости меридиана. Подобным же образом спроектируем и параллели. При этом каждая параллель, кроме экватора, как бы растягивается до размеров экватора.
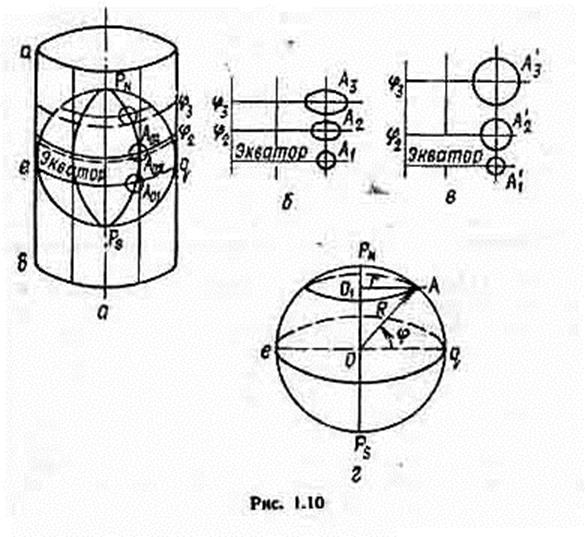
Выясним закон растяжения параллелей. Из рис. 1.10, г (прямоугольный треугольник ОАО1) видно, что
r = R cos j; R = r sin j, (1.4)
где R - радиус Земли; r - радиус параллели в широте j.
Умножим обе части равенства (1.4) на 2p. Получим 2pR = 2pr sec j, где 2pR - длина экватора; 2pr - длина параллели в широте j.
Следовательно, параллель, удлиняясь до длины экватора, растягивается пропорционально sec j. Чем больше широта параллели, тем меньше ее длина и тем больше она растягивается при переносе ее на цилиндр. Если после этого разрезать цилиндр по любой из образующих, например по ab, и развернуть цилиндр на плоскость, получившаяся на этой плоскости картографическая сетка будет иметь вид взаимно перпендикулярных прямых линий (рис. 1.10, б). Экватор при проектировании на цилиндр не растягивается, поэтому элементарно малый круг, расположенный на нем в точке А01 изобразится таким же кругом на карте - кругом А1. Произвольная параллель j2 растянута (искажена), поэтому элементарно малый круг А02, расположенный на этой параллели, изобразится на карте вытянутым вдоль параллели эллипсом А2. Чем больше широта j, тем больше растяжение параллели и, следовательно, тем сильнее проявляется искажение круга при его переносе на плоскость. Это значит, что требование равноугольности не выполнено. Чтобы проекция обладала свойством равноугольности, необходимо меридианы в каждой точке вытянуть пропорционально растяжению параллели этой точки. Удлинение меридианов в широте j должно быть таким, чтобы эллипс А2 превратился в круг А2' (рис. 1.10, 6). Чем больше широта, тем сильнее растянута параллель и, следовательно, тем больше должен быть вытянут меридиан. В результате одинаковые элементарно малые круги, расположенные на различных параллелях условного глобуса, изобразятся на карте кругами разных размеров, увеличивающихся с широтой. Это свидетельствует о том, что масштаб полученной карты изменяется пропорционально широте. По этой причине остров Гренландия на карте в меркаторской проекции изображается по размерам примерно таким же, как Африка, хотя в действительности ее площадь в 15 раз больше площади Гренландии.
Полученная таким образом проекция является прямой (ось цилиндра совмещена с осью Земли), равноугольной (элементарно малый круг на Земле изображается кругом на карте), цилиндрической (меридианы и параллели - взаимно перпендикулярные прямые).
Можно ли построить меркаторскую проекцию для приполюсяых участков Земли?
При j=90° (sec j = ¥) меридианы вытягиваются бесконечно. Прямую меркаторскую проекцию для приполюсных участков Земли построить невозможно. Карты приполюсных участков можно выполнить в поперечной меркаторской проекции, для которой j = 0°, sec j = 1. При построении и использовании карт в данной проекции применяется система квазигеографических координат.
Вертикальной (боковой) рамкой карты, выполненной в меркаторской проекции, является шкала широты. Известно, что одна минута широты соответствует длине морской мили. Следовательно, шкала широты одновременно является и шкалой линейных единиц длины, выраженных в морских милях.
Длина географического изображения одной минуты широты на меркаторской проекции называется меркаторской милей.
В соответствии с принципами построения меркаторской проекции меркаторская миля, являясь масштабным отображением морской стандартной мили, увеличивается с увеличением широты.
При измерении расстояний на карте необходимо пользоваться шкалой вертикальной рамки в том диапазоне широт, в котором находится измеряемый отрезок.
Горизонтальной (нижней или верхней) рамкой карты, выполненной в меркаторской проекции, является шкала долготы.
Длина одной минуты дуги земного экватора называется экваториальной или географической милей. Длина экваториальной мили равна D|Э' = RЭ arc 1' = 6378245 (1 / 3437,75) = 1855,36 м.
Радиус RЭ экватора - величина постоянная, поэтому экваториальная миля также постоянна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.