В полярной системе координат место заданной точки определяется по направлению и расстоянию относительно другой точки. Чаще всего полярная система координат применяется при определении места корабля относительно подвижного объекта.
При переходе корабля морем его место непрерывно изменяется. В связи с этим изменяются я географические координаты корабля. Изменение географических координат определяется разностью географических широт и разностью географических долгот.
Если рассматривается плавание корабля из точки О1 в точку О2 (рис. 1.6), то за начальную точку принимается пункт отхода (точка О1), а за конечную - пункт прихода (точка О2).
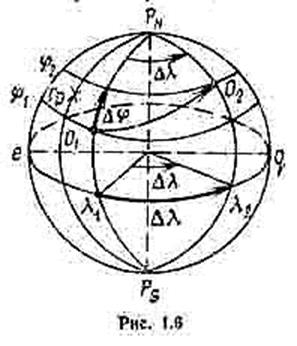
Разностью широт (РШ или Dj) двух заданных точек называется меньшая дуга меридиана, заключенная между параллелями этих точек. Дуга, определяющая разность широт, направлена от параллели начальной точки к параллели конечной точки. Если это направление совпадает с направлением на Северный географический полюс, то независимо от полушария, в котором находятся точки, РШ имеет наименование North (к N) или знак "плюс". Если дуга меридиана направлена на Южный географический полюс, то РШ имеет наименование South (к S) или знак "минус".
РШ и ее знак определяются по алгебраической формуле
РШ = Dj = j1 - j2. (1.2)
РШ изменяется в пределах от 0 до ± 180°.
Разностью долгот (РД или Dl) двух заданных точек называется меньшая дуга экватора, заключенная между меридианами этих точек. Дуга, определяющая разность долгот, направлена от меридиана начальной точки к меридиану конечной точки. Если это направление совпадает с направлением на восток, то независимо от полушария, в котором находятся точки, РД имеет наименование Еаst (к E) или знак "плюс". Если дуга экватора направлена на запад, то РД имеет наименование West (к W) или знак "минус".
РД и ее знак рассчитываются по алгебраической формуле
РД = Dl = l1 - l2. (1.3)
РД изменяется в пределах от 0 до 180°.
Если результат расчета по формуле (1.3) окажется больше 180°, то искомая РД равна дополнению полученного результата до 360°, при этом полученный по формуле знак меняется на противоположный.
Формулы (1.2) и (1.3), представленные в виде равенств:
j2 = j1 + РШ = j1 + Dj;
l2 = l1 + РД = l1 + Dl,
используются для расчета координат конечной точки.
Решение основных задач кораблевождения связано с определением линий (траекторий), проходящих через две заданные точки на земной поверхности и удовлетворяющих определенным требованиям. Такими линиями являются ортодромия и локсодромия.
1.4.1 Ортодромия
На поверхности сферы кратчайшим расстоянием между двумя точками является дуга большого круга, образованного пересечением плоскостью, проходящей через центр сферы и заданные точки, сферической поверхности.
Дуга большого круга в кораблевождении называется ортодромией (в переводе с греческого - "прямой путь").
Через три точки (две заданные на поверхности Земли и центр Земли-шара) можно провести только одну плоскость. Следовательно, через две точки на земной поверхности В1 (j1, l1) и B2 (j2, l2) можно провести только одну ортодромию МВ1В2V (рис. 1.7). Уравнение ортодромии, связывающее координаты точек, лежащих на ней, определяется по формуле сферической тригонометрии.
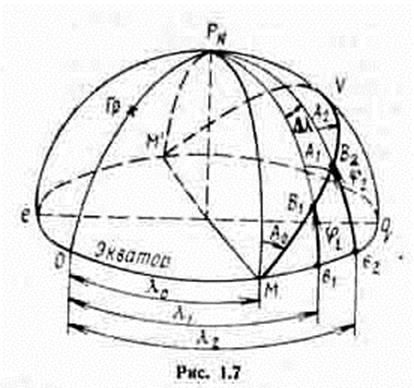
Из рис. 1.7 следует, что при направлении А0=0° (точки В1 и В2 на одном меридиане) ортодромия совпадает с меридианом, при А0=90° (точки В1 и В2 на экваторе) ортодромия совпадает с экватором. Ортодромия достигает максимальной широты в точке V, называемой вертексом. Меридиан вертекса является осью симметрии ортодромии. Ортодромия пересекает каждый меридиан только один раз (в одной точке). Одна и та же ортодромия пересекает меридиан под разными углами (А0¹А1¹А2). Разность углов, под которыми ортодромия пересекает меридианы двух точек, называется сближением меридианов g. Угол сближения меридианов точек В1 и В2 равен g = А2 - А1.
Ортодромия используется при расчете плавания по кратчайшему пути, а также при определении места корабля по радиопеленгам.
1.4.2 Локсодромия
Локсодромия - кривая на поверхности Земли, пересекающая все меридианы под одним и тем же углом К (рис. 1.8). Локсодромия - греческое слово, означающее "кривой путь". Эта линия представляет собой траекторию пути корабля, совершающего плавание в неизменном направлении относительно всех меридианов.
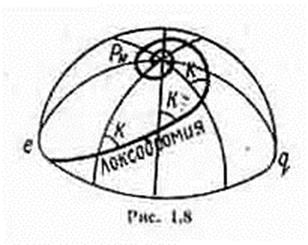
При К=0° (180°) локсодромия совпадает с меридианом и ортодромией. При К=90° (270°) локсодромия совпадает с параллелью.
При любых других курсах локсодромия пересекает каждый меридиан бесчисленное множество раз и каждый раз в новой широте, т. е. локсодромия является логарифмической спиралью, стремящейся к полюсу.
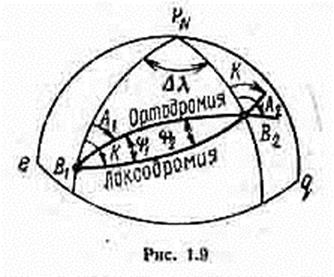
Если через заданные точки В1 (j1, l1) и В2 (j2, l2) провести ортодромию и локсодромию (рис. 1.9), то эти кривые пересекутся под некоторым углом y(А1¹К). Этот угол называется ортодромической поправкой. Она служит для перехода от ортодромических направлений к локсодромическим и обратно:
Лок П = Орт П + y; Орт П = Лок П - y.
Значения ортодромической поправки приведены в табл. 23а, 23б МТ-75.
Для решения навигационных задач, связанных с движением и ориентированием корабля на водной поверхности Земли, необходимо измерять и рассчитывать расстояния. В качестве морской единицы длины в кораблевождении используют так называемую стандартную морскую милю, то есть среднюю величину одной минуты меридиана земного эллипсоида.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.