Фоновые напряжения в ферменных конструкциях из композитов, страница 2

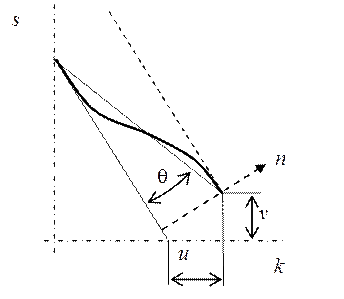
Рис.2. К расчету изгибающего момента в спиральном ребре

В силу линейности деформирования результирующее напряженно-деформированное состояния можно представить как сумму решений двух задач: рассмотренной выше задачи о безмоментном деформировании ребер (с рассогласованием углов поворота сечений спиральных ребер по отношению к кольцевым) и задачи о деформировании спирального ребра при повороте крайних сечений на угол .

Вычислим угол . Найдем перемещения нижнего (см. рис. 2) конца спирального ребра относительно верхнего:

, .                                                                                       (7)

В силу малости угла  можно считать, что он равен своему тангенсу, который, в свою очередь, равен проекции вектора (u, v) на нормаль к ребру, отнесенной к длине ребра:

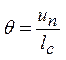.                                                                                                                (8)

Перемещение по нормали к ребру найдем, зная координаты вектора перемещений в осях (k, s) и углы между этими осями координат и нормалью n:

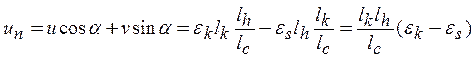.                              (9)

Тогда с учетом формул (4) и (6) имеем:

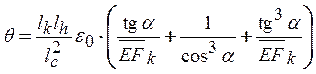,                                                              (10)

откуда после тождественных преобразований получаем:

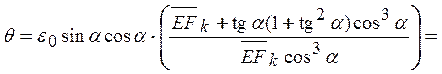
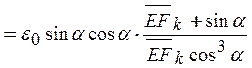.                                                                           (11)

Рассмотрим, далее, упругое деформирование ребра при заданных углах поворота опорных сечений q* (рис. 3).

 

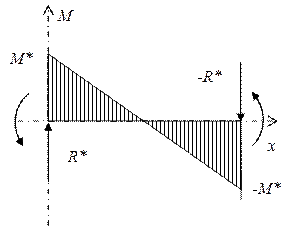
Рис.3. Схема деформирования ребра при заданных поворотах опорных сечений и эпюра изгибающего момента

Примем для описания деформации ребра модель балки Тимошенко. Производная от прогиба по осевой координате балки x равна сумме угла поворота сечения и угла поперечного сдвига:

,                                                                                                            (12)

которые определяются физическим законом:

, ,                                                                                 (13)

где

EI – изгибная жесткость,

I – момент инерции,

G – модуль сдвига,

F – площадь сечения ребра,

GF - жесткость на поперечный сдвиг,

M, Q – изгибающий момент и поперечная сила в сечении.

Из условий равновесия

,                                                                                                  (14)

с учетом физического закона (13) и кинематической связи (12) получаем разрешающие дифференциальные уравнения. Учитывая, что в соответствии с (14) момент является линейной функцией координаты, а в силу симметрии опорные моменты M* равны, найдём:

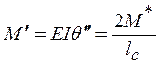,                                                                                             (15)

откуда

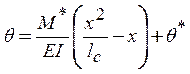.                                                                                       (16)

Опорные реакции найдем из условия интегрального равновесия:

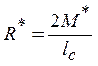.                                                                                                          (17)

Тогда из физического закона можно найти угол сдвига 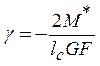, что после подстановки в (12) дает дифференциальное уравнение для прогиба:

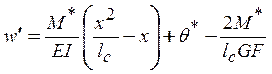.                                                                       (18)

В этом уравнении величина опорного момента M* неизвестна. Проинтегрируем его с граничными условиями: ; одно условие используем для определения константы интегрирования, а второе – для определения опорного момента:

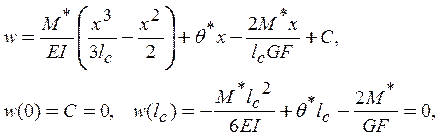                                      (19)

откуда окончательно получаем:

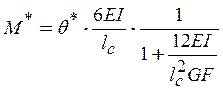.                                                                                 (20)

Таким образом, максимальные напряжения, обусловленные изгибом спирального ребра, равны

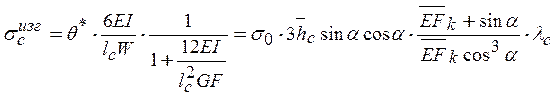,              (21)

где угол поворота опорных сечений определяется выражением (11),

W – момент сопротивления сечения,

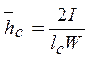 - безразмерный параметр.

ИЗГИБ КОЛЬЦЕВЫХ РЕБЕР

Кольцевые ребра нагружены радиальными силами в точках соединения со спиральными. Эти силы, схема приложения которых показана на рисунке 4 (слева), вызывают изгиб каждого участка кольцевого ребра моментом, эпюра которого показана на том же рисунке справа тонкой линией. В местах соединения ребер растянутыми оказываются внешние волокна, на серединах кольцевых ребер – внутренние волокна ребра, которое изображено на этом рисунке жирной линией.

Рис. 4. Схема нагружения кольцевого ребра в плоскости окружности и эпюра изгибающего момента

Как видно из рисунка 4, отрезок кольцевого ребра между точками соединения со спиральными нагружен силами Q и N, равнодействующая которых T направлена по касательной к оси кольцевого ребра в точке, находящейся посередине этого отрезка (точка А на рисунке; касательная показана штрих-пунктирной линией). В точке А сила T уравновешивается внутренней продольной силой, растягивающей ребро. Изгибающий момент в точке соединения ребер В равен моменту в точке А плюс момент продольной силы, приложенной в этой точке, относительно точки соединения:

,                                                                                         (22)

где l – плечо силы.

Поскольку продольная сила известна, можно найти распределение момента по длине ребра при произвольном значении момента в точке А. Введем криволинейную систему координат, в которой s равно длине дуги окружности от точки А до текущей точки оси ребра. Плечо l в текущей точке s равно расстоянию от точки до касательной, проведенной в точке А:

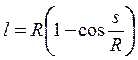,                                                                                                  (23)

где R – радиус цилиндрической оболочки.

Тогда имеем:

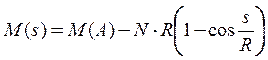.                                                                        (24)

Учитывая, что концевые сечения не поворачиваются; это позволит найти момент в точке А. Будем считать ребро тонким криволинейным стержнем (высота сечения не превышает 1/5 радиуса). С учетом физического закона (13) имеем:

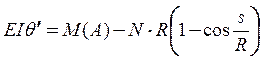,                                                                         (25)

откуда после интегрирования с учетом граничного условия

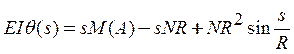.                                                                   (26)

Значение координаты s в точке В равно 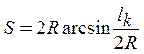. Найдем М(А) из условия: . Приравняв нулю правую часть (26), получим:

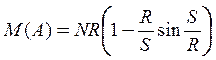.                                                                                  (27)

Подставив значение S, получим после тригонометрических преобразований:

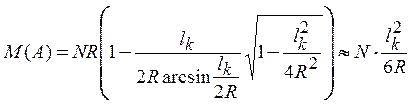.                                           (28)

Приближенное выражение найдено разложением в ряд по степеням длины отрезка кольцевого ребра . Момент в точке В найдём из (24) с учетом полученного выражения (28):