УДК 539.3
ФОНОВЫЕ НАПРЯЖЕНИЯ В ФЕРМЕННЫХ КОНСТРУКЦИЯХ ИЗ КОМПОЗИТОВ *
В.О. КАЛЕДИН, Т.В. БУРНЫШЕВА, А.Б. МИТКЕВИЧ
В статье рассматривается задача расчетно-теоретического анализа фоновых напряжений в оребренных оболочечных конструкциях при отсутствии обшивки. Предложена двухуровневая математическая модель, основанная на аналитическом решении идеализированной задачи и получении поправок путем полного дискретного моделирования оребрения конструкции. Практическая значимость полученных результатов заключается в построении методики расчета напряжений в конструкциях типа ферм, состоящих из коротких стержней из композиционных материалов.
Ключевые слова: ферменные конструкции, композиционные материалы, фоновые напряжения, напряженно-деформированное состояние, концентрация напряжений, дискретная модель.
Среди силовых конструкций из полимерных композиционных материалов большое распространение имеют конструкции типа оребренных оболочек, особенностями которых является регулярная система спиральных и кольцевых ребер. Эти конструкции обладают рядом преимуществ перед оболочечными конструкциями, подкрепленными продольно-поперечным силовым набором.
В случае однородного напряженного состояния, не изменяющегося или слабо изменяющегося по поверхности оболочки, она может быть описана на основе континуальной модели, предполагающей осреднение оребренной структуры по поверхности конструкции. Однако, наличие вырезов конструктивного и технологического назначения приводит к возникновению концентраций напряжений в их окрестности. Континуальная модель в этом случае резко завышает реальные напряжения в углах отверстий.
Избежать появления сингулярностей подобного типа позволяет модель, основанная на полном дискретном моделировании ребер. Использование такой модели дает реальную картину полей напряжений в окрестности вырезов.
Для выбора рациональных размеров и формы отверстий необходимо провести исследование коэффициентов концентрации напряжений при варьировании параметров оболочки. В качестве коэффициентов концентрации рассматриваются отношения максимальных значений напряжений к фоновым напряжениям такой же конструкции без вырезов. В связи с этим необходим глубокий анализ фоновых напряжений, рассчитанных на основе аналитических и численно-аналитических методов.
Объектом исследования является цилиндрическая оболочка из углепластика с оребренной структурой. В средней части оболочки может находиться вырез – некомпенсированный либо усиленный окантовкой. Вдоль образующей оболочка нагружена сжимающей силой.
За координатную поверхность конструкции выбирается срединная поверхность ребер. Напряжения будем относить к криволинейной системе координат (s, t, n), в которой ось n направлена по нормали к поверхности оболочки, ось t – по окружности и ось s – вдоль образующей.
Дискретная модель оребренной оболочки строится на основе треугольника Зенкевича для обшивки и балки типа Тимошенко для ребер. Такой выбор обусловлен тем, что ребра имеют высоту сечения, соизмеримую с размером треугольной ячейки, и представляют собой, таким образом, короткую балку, для которой существенно влияние сдвиговых деформаций на напряженное состояние; напротив, обшивка является достаточно тонкой, чтобы её можно было описывать в рамках гипотез Кирхгофа-Лява.
Высота сечений ребер в численных расчетах принималась постоянной и не варьировалась. Ширина сечений всех ребер одного семейства – кольцевых или спиральных – принималась одинаковой, причем варьировались как площади сечений спиральных и кольцевых ребер, так и их соотношение.
Для получения аналитического решения задачи о деформировании оребренной структуры рассмотрим плоскую неограниченную двоякопериодическую систему горизонтальных и диагональных ребер, нагруженную вдоль вертикали. После сворачивания в цилиндр горизонтальные ребра переходят в кольцевые, а диагональные – в спиральные ребра. Поэтому в дальнейшем не будет делаться различие между кольцевыми и горизонтальными, а также между диагональными и спиральными ребрами.
Для определения продольных усилий в ребрах рассмотрим равновесие элементарной треугольной ячейки, схема нагружения которой приведена на рисунке 1.
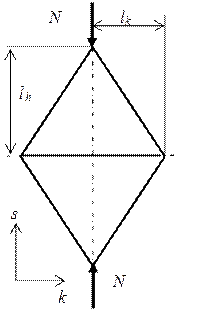
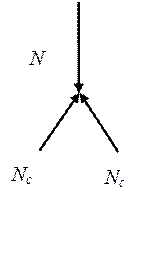
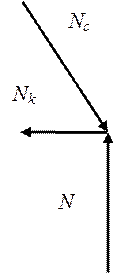
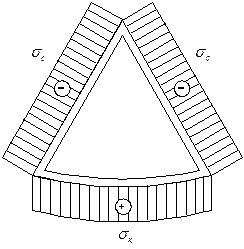
Рис. 1. Схема нагружения треугольной ячейки, равновесие сил и эпюра средних напряжений в ребрах
Обозначим через N внешнюю сжимающую силу, приходящуюся на пару спиральных ребер. Тогда из равновесия сил получим сжимающую силу в спиральном ребре Nc и растягивающую силу в кольцевом ребре Nk. Силы, действующие в ребрах, определяются как произведения средних напряжений на площади сечений ребер. На рисунке 1 показаны эпюры средних напряжений в ребрах, из которых видно их растяжение и сжатие. Величины сил в спиральных и кольцевых ребрах рассчитываются следующим образом:
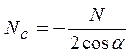 ,
, 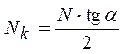 , (1)
, (1)
где ![]() - угол между спиральным ребром и
образующей:
- угол между спиральным ребром и
образующей:
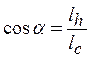 ,
, 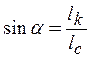 ,
,
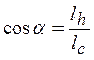 ,
, ![]() . (2)
. (2)
Пусть продольный модуль упругости спиральных и кольцевых ребер равен Ec и Ek соответственно, площади сечений Fc и Fk. Тогда продольные деформации ребер
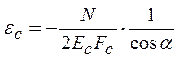 ,
, 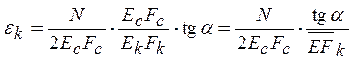 . (3)
. (3)
Безразмерный
комплекс 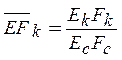 характеризует жесткость кольцевых ребер
по отношению к спиральным, а комплекс
характеризует жесткость кольцевых ребер
по отношению к спиральным, а комплекс 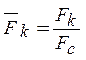 -
отношение площадей сечений кольцевых и спиральных ребер.
-
отношение площадей сечений кольцевых и спиральных ребер.
Ведем обозначения:
![]() =
=![]() -
величина характеризует интенсивность нагрузки;
-
величина характеризует интенсивность нагрузки;
![]() =
=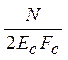 -
величина характеризует деформацию.
-
величина характеризует деформацию.
С учетом обозначений, для средних по сечению напряжений в ребрах и продольных деформаций ребер имеем:
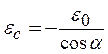 ,
, 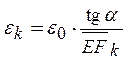 ,
,
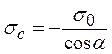 ,
, 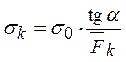 . (4)
. (4)
Найдем
осевую деформацию ячейки. В осях (s, k),
связанных с ячейкой (см. рис. 1), угловая деформация равна нулю, т.е.
деформации ![]() и
и ![]() –
главные деформации. Линейная деформация в направлении спирального ребра,
составляющем угол
–
главные деформации. Линейная деформация в направлении спирального ребра,
составляющем угол ![]() с осью s,
определится по формуле поворота базиса следующим образом:
с осью s,
определится по формуле поворота базиса следующим образом:
![]() , (5)
, (5)
откуда
найдём ![]() :
:
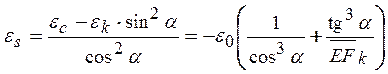 . (6)
. (6)
Эти результаты являются точными, поскольку получены только на основе условий равновесия. Однако они не учитывают изгиба спиральных ребер.
Для
вычисления изгибающих моментов примем во внимание, что соединения ребер не
являются шарнирными; деформирование по использованной выше схеме нарушает
кинематическую совместность, поскольку спиральные ребра поворачиваются при
деформации на угол ![]() (рис. 2).
(рис. 2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.