Контрольные вопросы:
1. Какая функция называется сеточной?
2. Какое уравнение называется разностным?
3. Какие уравнения называются разностными уравнениями 1-го порядка?
4. Как находится общее решение неоднородного разностного уравнения 1-го порядка?
5. Какое решение разностного уравнения называется фундаментальным?
6. Почему общее решение однородного уравнения с постоянными коэффициентами имеет вид геометрической прогрессии?
Задания.
1. Написать процедуру решения разностного уравнения первого
порядка ![]() с начальным условием
с начальным условием ![]() .
.
2. Для заданного уравнения найти общее и частное решение аналитически.
3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.
4. Выяснить, как влияет на результат возмущение начального условия, коэффициентов уравнения, правой части.
|
|
А |
В |
Указания |
|
|
1 |
|
|
2 |
|
|
2 |
|
0 |
2 |
|
|
3 |
1 |
1 |
2 |
|
|
4 |
n |
1 |
2 |
|
|
5 |
|
3 |
2 |
|
|
6 |
|
|
1 |
|
|
7 |
|
0 |
1 |
|
|
8 |
1 |
1 |
1 |
|
|
9 |
n |
1 |
1 |
|
|
10 |
|
3 |
1 |
|
|
11 |
|
|
|
|
|
12 |
|
0 |
|
|
|
13 |
1 |
1 |
|
|
|
14 |
n |
1 |
|
|
|
15 |
|
3 |
|
Рекомендации к выполнению задания.
Найдем общее решение разностного уравнения 1-го порядка
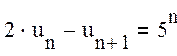 . (1)
. (1)
Частное решение однородного уравнения при ![]() получим, используя рекуррентную формулу:
получим, используя рекуррентную формулу: ![]() . Поскольку значение Y в каждом следующем узле сетки
удваивается, получается геометрическая прогрессия со знаменателем q=2:
. Поскольку значение Y в каждом следующем узле сетки
удваивается, получается геометрическая прогрессия со знаменателем q=2:
![]() .
.
Частное решение неоднородного уравнения найдем в виде:![]() , где А - неопределенный коэффициент.
Тогда
, где А - неопределенный коэффициент.
Тогда ![]() ,
, 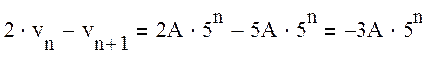 ,
и, приравняв полученное значение к заданной правой части, найдем неопределенный
коэффициент A=
,
и, приравняв полученное значение к заданной правой части, найдем неопределенный
коэффициент A=![]() . Окончательно, общее
решение:
. Окончательно, общее
решение: 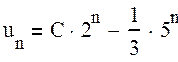 .
.
Используя
начальное условие ![]() , находим константу:
, находим константу: 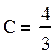 . Окончательно, частное решение при заданном начальном
условии:
. Окончательно, частное решение при заданном начальном
условии:
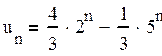 .
.
Для исследования устойчивости решения к возмущению самого решения и начального условия рассмотрим следующее уравнение:
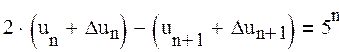
с возмущенным начальным условием ![]()
(здесь ![]() - величина
возмущения). Вычитая исходное уравнение (1), получим разностное уравнение для
возмущения:
- величина
возмущения). Вычитая исходное уравнение (1), получим разностное уравнение для
возмущения:
![]()
с
начальным условием ![]() .
Решение этого уравнения имеет вид:
.
Решение этого уравнения имеет вид: 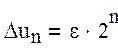 , т.е. даже малое возмущение в каком-либо узле экспоненциально растет с
увеличением номера узла.
, т.е. даже малое возмущение в каком-либо узле экспоненциально растет с
увеличением номера узла.
Студенту необходимо проиллюстрировать сказанное выше: исследовать влияние возмущений начального условия, правых частей и коэффициентов уравнения, изменив рекуррентную формулу.
Вариант, в соответствии с номером студента по списку в журнале, необходимо решить на языке программирования C++ (допускается использование среды Builder) или Pascal (допускается использование среды Delphi).
Содержание отчета должно быть следующим:
а) при возмущении начального условия;
б) при возмущении коэффициентов уравнения;
в) при возмущении правой части.
Тема :Разностные уравнения 2 порядка
Контрольные вопросы:
1. Какие уравнения называются разностными уравнениями 2-го порядка?
2. Что такое характеристическое уравнение?
3. Как выглядит частное решение однородного разностного уравнения 2-го порядка с действительными корнями характеристического уравнения?
4. Как выглядит частное решение однородного разностного уравнения 2-го порядка с комплексными корнями характеристического уравнения?
5. Как находится общее решение неоднородного разностного уравнения 2-го порядка?
6. Что такое численное и аналитическое решение разностного уравнения 2-го порядка?
7. Какие задачи называются хорошо обусловленными?
Задания
1.
Написать процедуру решения
разностной краевой задачи для уравнения второго порядка ![]() с
граничными условиями
с
граничными условиями ![]() ,
, ![]() .
.
2. Для заданного уравнения найти общее и частное решение аналитически и проверить критерий обусловленности.
3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.
4. Выяснить, как влияет на результат возмущение граничных условий и правой части.
|
№ |
|
А |
В |
a |
b |
c |
|
1 |
|
|
2 |
1 |
-2 |
1 |
|
2 |
|
0 |
2 |
2 |
4 |
1 |
|
3 |
1 |
1 |
2 |
1 |
3 |
1 |
|
4 |
n |
1 |
2 |
5 |
-26 |
5 |
|
5 |
|
3 |
2 |
2 |
5 |
2 |
|
6 |
|
|
1 |
2 |
5 |
2 |
|
7 |
|
0 |
1 |
5 |
-26 |
5 |
|
8 |
1 |
1 |
1 |
2 |
5 |
2 |
|
9 |
n |
1 |
1 |
1 |
3 |
1 |
|
10 |
|
3 |
1 |
1 |
3 |
1 |
|
11 |
|
|
|
2 |
4 |
1 |
|
12 |
|
0 |
|
1 |
-2 |
1 |
|
13 |
1 |
1 |
|
2 |
5 |
2 |
|
14 |
n |
1 |
|
2 |
5 |
2 |
|
15 |
|
3 |
|
1 |
3 |
1 |
Рекомендации к выполнению задания
Найдем общее решение разностного уравнения 2-го порядка
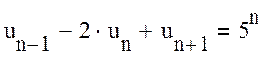 . (1)
. (1)
Запишем характеристическое уравнение:
![]() .
.
Поскольку корни ![]() совпали, то частные решения
однородного уравнения имеют вид (8), (9):
совпали, то частные решения
однородного уравнения имеют вид (8), (9):
![]() ,.
,.
Частное решение неоднородного уравнения найдем в виде:
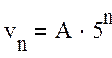 , где А
- неопределенный коэффициент. Подставив это выражение в исходное уравнение,
получим:
, где А
- неопределенный коэффициент. Подставив это выражение в исходное уравнение,
получим:
![]() ,
,
откуда ![]() ,
, 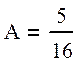 , и
окончательно, общее решение:
, и
окончательно, общее решение:
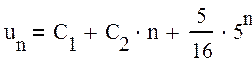 .
.
Теперь любое частное решение при заданных начальных
условиях ![]() можно найти выбором произвольных постоянных
можно найти выбором произвольных постоянных
![]() .
.
Наряду
с задачами Коши, для уравнений 2-го порядка рассматриваются также двухточечные
краевые задачи, в которых заданы значения сеточной функции в двух узлах,
расположенных не подряд, а на концах некоторого конечного отрезка: ![]() (граничные условия).
Аналитическое решение такой задачи можно получить подходящим выбором
произвольных постоянных в общем решении. Однако, в отличие от задачи с
начальными условиями, краевая задача не обязательно будет однозначно
разрешимой. Поэтому большое значение имеет выяснение класса краевых задач,
которые обладают однозначной разрешимостью и слабой чувствительностью к
возмущению (вследствие ошибок округления) правых частей и граничных условий.
Такие задачи будем называть хорошо обусловленными
(граничные условия).
Аналитическое решение такой задачи можно получить подходящим выбором
произвольных постоянных в общем решении. Однако, в отличие от задачи с
начальными условиями, краевая задача не обязательно будет однозначно
разрешимой. Поэтому большое значение имеет выяснение класса краевых задач,
которые обладают однозначной разрешимостью и слабой чувствительностью к
возмущению (вследствие ошибок округления) правых частей и граничных условий.
Такие задачи будем называть хорошо обусловленными
Рассмотрим пример плохо обусловленной краевой задачи
![]() ,
, ![]() (2)
(2)
и придадим правым частям малые приращения:
![]() .
.
Тогда решение получит приращение, определяемое из вспомогательной краевой задачи
![]() ,
, ![]() . (3) Решение
задачи (3) несложно получить аналитически:
. (3) Решение
задачи (3) несложно получить аналитически:
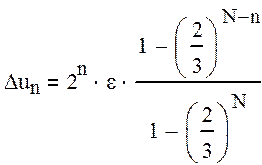
В частности, при n=N-1 имеем: 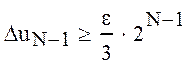 , т.е. возмущение решения быстро растет с увеличением
числа узлов N. Оценка хорошей обусловленности задачи, которая рассматривается в
курсе лекций, не выполняется (проверьте!).
, т.е. возмущение решения быстро растет с увеличением
числа узлов N. Оценка хорошей обусловленности задачи, которая рассматривается в
курсе лекций, не выполняется (проверьте!).
Один вариант, в соответствии с заданием, полученным от преподавателя, необходимо решить на языке программирования C++ (допускается использование среды Builder) или Pascal (допускается использование среды Delphi).
Содержание отчета должно выглядеть следующим образом:
а) при возмущении начального условия;
б) при возмущении правой части.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.