На ошибках учатся только те, кто не путает их с победами
Линейная независимость
Введение
Существует две задачи:
1. Дан базис, надо построить линейную оболочку.
Один
из хороших способов задания линейного пространства – это задать систему ![]() , тогда
, тогда ![]()
![]() , где
, где ![]() –
числа. И все такие
–
числа. И все такие ![]() образуют линейное
пространство. Это техника от базиса.
образуют линейное
пространство. Это техника от базиса.
Пример. Даны два
непараллельных вектора ![]() .
.
Задавая
![]() ,
,![]() точки
будут пробегать всю плоскость
точки
будут пробегать всю плоскость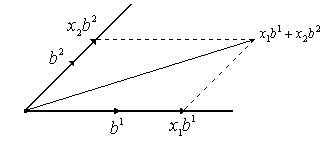 , следовательно, плоскость – это линейная оболочка двух непараллельных
векторов.
, следовательно, плоскость – это линейная оболочка двух непараллельных
векторов.
2. Дано линейное пространство, надо определить базис.
Пусть имеется элемент ![]() линейной
оболочки системы векторов
линейной
оболочки системы векторов ![]() , тогда его можно
представить в виде линейной комбинации этих векторов:
, тогда его можно
представить в виде линейной комбинации этих векторов: 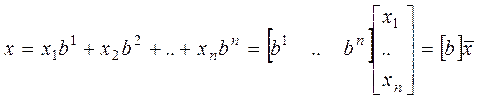 .
.
При изоморфизме нулевому элементу ![]() соответствует нулевой элемент
соответствует нулевой элемент ![]() . Действительно, если
. Действительно, если ![]() , то
, то![]() т.
о.
т.
о. ![]() , а значит,
, а значит, ![]() .
.
Тогда
в системе векторов ![]() элементу
элементу ![]() однозначно соответствует элемент
однозначно соответствует элемент ![]() :
: ![]() .
.
Изоморфизм должен сохранять операции. Проверим.
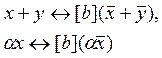
![]() – тензор элемента
– тензор элемента ![]() (его координата).
(его координата).
Геометрический изоморфизм мы уже установили (см. лекцию 15).
Пусть имеется линейная оболочка системы ![]() , т. к.
, т. к. ![]() –
есть линейное пространство, то оно содержит нулевой элемент:
–
есть линейное пространство, то оно содержит нулевой элемент:
![]() – тривиальная линейная комбинация.
– тривиальная линейная комбинация.
![]() Система элементов
Система элементов ![]() называется линейно независимой,
если нулевой элемент представляется только тривиальной комбинацией
называется линейно независимой,
если нулевой элемент представляется только тривиальной комбинацией ![]() , а если другой, то линейно зависимой.
, а если другой, то линейно зависимой.
Или,
если ни один из ![]() не представляется линейной
комбинацией других, то система линейно независима.
не представляется линейной
комбинацией других, то система линейно независима.
Теорема.
Если
система ![]() линейно независимая, то всякий
элемент
линейно независимая, то всякий
элемент ![]() линейной оболочки:
линейной оболочки:![]() представляется единственной линейной
комбинацией. (Если
представляется единственной линейной
комбинацией. (Если ![]() линейно зависимая, то
нет.)
линейно зависимая, то
нет.)
Доказательство. Пусть ![]() и
и ![]() .,
тогда
.,
тогда
![]() . Т. к. система
. Т. к. система ![]() линейно независимая, то нулевой
элемент представляется только тривиальной комбинацией, следовательно,
линейно независимая, то нулевой
элемент представляется только тривиальной комбинацией, следовательно, ![]() . Значит, разложение единственно.//
. Значит, разложение единственно.//
Типовая задача 1установить линейную независимость данного набора векторов линейного пространства.
Пусть
в линейном пространстве найдется ![]() – линейно независимых
элементов, а всякий
– линейно независимых
элементов, а всякий ![]() – элемент делает систему
линейно зависимой, тогда
– элемент делает систему
линейно зависимой, тогда ![]() – размерность
пространства, а сама система векторов является базисом пространства.
– размерность
пространства, а сама система векторов является базисом пространства.
Замечание базис пространства определен неоднозначно.
3.
Линейная независимость в ![]()
·
![]() :
элемент
:
элемент ![]() из
из ![]() является
базисом, т. к. всякое другое число есть элемент
является
базисом, т. к. всякое другое число есть элемент ![]() ,
умноженный на некоторое число.
,
умноженный на некоторое число.
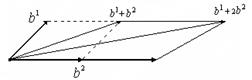
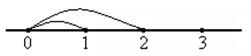 2=1+1,
2=1+1,
3=2+1 по правилу параллелограмма.
0=0*1-тривиальная комбинация.
·
![]() :
элементы
:
элементы 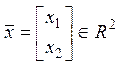 .
.
Например,
имеется два линейно независимых элемента: 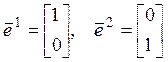 .
Действительно, выразим
.
Действительно, выразим ![]() через
через ![]() :
: 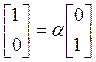 ,
но система
,
но система 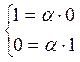 решений не имеет, а значит элементы
линейно независимы.
решений не имеет, а значит элементы
линейно независимы.
Всякий
третий элемент 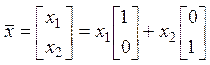 делает систему линейно
зависимой:
делает систему линейно
зависимой:
![]() (коэффициент при
(коэффициент при ![]() не равен нулю).
не равен нулю).
В нулевой линейной комбинации либо все коэффициенты равны нулю, либо минимум два коэффициента не равны.
Т.
о. ![]() .
.
· ![]() : элементы
: элементы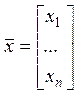 .
.
Рассмотрим
систему элементов 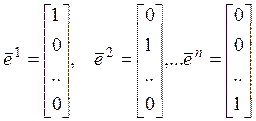 , тогда любой элемент
, тогда любой элемент ![]() можно представитьлинейной
комбинацией
можно представитьлинейной
комбинацией![]() :
: 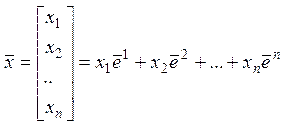 . Будет ли система
. Будет ли система ![]() базисом?
базисом?
1.
Рассмотрим линейную комбинацию ![]() , если все
, если все ![]() ,
то система линейно независимая.
,
то система линейно независимая. 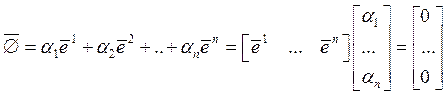 – однородная
система.
– однородная
система. 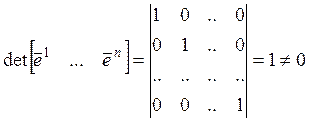 , следовательно, Крамеровская
система, а значит, система имеет единственное решение
, следовательно, Крамеровская
система, а значит, система имеет единственное решение ![]() .
.
Вывод (условие линейной независимости в ![]() ): если определитель,
составленный из координат векторов, не равен нулю, то вектора линейно независимы.
Если равен нулю, то линейно зависимы.
): если определитель,
составленный из координат векторов, не равен нулю, то вектора линейно независимы.
Если равен нулю, то линейно зависимы.
2.
Система ![]() –
линейно зависимая, т. к.
–
линейно зависимая, т. к. ![]() – нетривиальная
комбинация.
– нетривиальная
комбинация.
Значит, ![]() – базис
– базис ![]() и тогда
и тогда ![]() .
.
Типовая задача 2разложить заданный вектор по заданной системе других векторов (как линейно независимых, так и линейно зависимых).
1.
Пространство ![]() – линейная оболочка вектора
– линейная оболочка вектора ![]() . Линейная оболочка одного аргумента
называется направлением.
. Линейная оболочка одного аргумента
называется направлением.
![]() Любой
элемент
Любой
элемент ![]() , но тогда
, но тогда ![]() –
нетривиальная комбинация, следовательно, они зависимы.
–
нетривиальная комбинация, следовательно, они зависимы.
Т. о. один
независим (![]() ), а остальные зависимы от него (в
школе – это коллинеарные вектора), в силу этого, в
), а остальные зависимы от него (в
школе – это коллинеарные вектора), в силу этого, в ![]() всякая
система двух векторов линейно зависима.
всякая
система двух векторов линейно зависима.
2.
Пространство ![]() , где
, где ![]() – векторы разного направления.
– векторы разного направления. ![]() называется
плоскостью векторов.
называется
плоскостью векторов.
 Любой элемент
Любой элемент ![]() можно
представить линейной комбинацией
можно
представить линейной комбинацией ![]() :
: ![]() .
.
Тогда ![]() – нетривиальная
комбинация, следовательно,
– нетривиальная
комбинация, следовательно, ![]() – базис. В
– базис. В ![]() (на плоскости)
любые три вектора линейно зависимы.
(на плоскости)
любые три вектора линейно зависимы.
Пусть дана система функций ![]() ,
, ![]() .
.
![]() (ограничим
регулярными функциями
(ограничим
регулярными функциями ![]() ).
).
Является ли система функций ![]() линейно
независимой?
линейно
независимой?
Если ![]() –
тривиальная комбинация, то да. Продифференцируем левую и правые части:
–
тривиальная комбинация, то да. Продифференцируем левую и правые части:
![]()
![]() ,
,
![]() ,
,
нам достаточно
продифференцировать ![]() раз:
раз:
![]() .
.
Перед нами однородная система, в матричном виде, которая имеет вид:
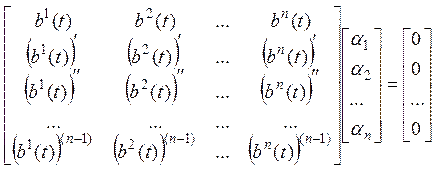 .
.
Однородная система всегда
разрешима (всегда имеется тривиальное решение), причем, решение будет
единственное, если определитель основной матрицы не равен нулю – условие
линейной независимости в ![]() :
:
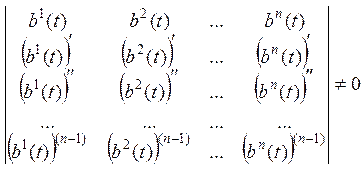 –
определитель Вронского.
–
определитель Вронского.
Пример. Дана система ![]() .
Является ли она линейно независимой?
.
Является ли она линейно независимой?
Составим определитель Вронского:
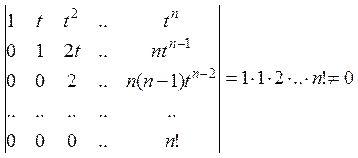 .
.
Значит, система элементов ![]() линейно независима
линейно независима ![]() , а следовательно, в пространстве
регулярных функций
, а следовательно, в пространстве
регулярных функций ![]() сколь угодно линейно
независимых функций.
сколь угодно линейно
независимых функций.
Т. о. линейные пространства подразделяют на конечномерные и бесконечномерные пространства.
Пример.
1.
Определить, является ли система
векторов в ![]() базисом?
базисом? 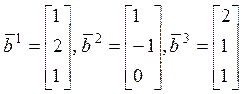 .
.
2.
Разложить вектор 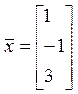 по системе
по системе ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.