Студент не посудина, которую надо заполнить, а факел, который надо зажечь.
Скалярное произведение
1. Определение
![]() Скалярное произведение –
это функционал типа
Скалярное произведение –
это функционал типа ![]() , т. е. любым векторам
, т. е. любым векторам ![]() ставится в соответствие пара
ставится в соответствие пара ![]() . (Аргументы – это векторы, значение
– число.)
. (Аргументы – это векторы, значение
– число.)
![]()
![]() –
функция,
–
функция, ![]() – преобразование,
– преобразование,![]() – функционал
– функционал![]()
При этом выполняются аксиомы:
1.
![]() –
симметрия (коммутативность),
–
симметрия (коммутативность),
2.
![]() –однородность.
В силу симметрии
–однородность.
В силу симметрии ![]() .
.
3.
![]() – аддитивность. Следовательно,
– аддитивность. Следовательно, ![]() , т. к.
, т. к. ![]() .
.
4.
![]() и
и ![]() – неотрицательность.
– неотрицательность.
Рассмотрим примеры скалярных произведений в различных пространствах.
· Скалярное произведение в арифметическом
пространстве ![]() .
.
Определим скалярное произведение
следующим образом: 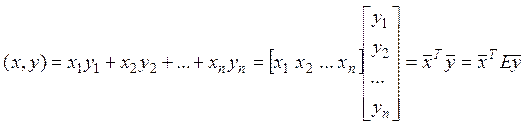 .
.
Очевидно, что все свойства скалярного произведения выполнены.
Замечание. Можно ввести скалярное произведение следующим
образом ![]() , где
, где ![]() .
Какими свойствами должна обладать матрица
.
Какими свойствами должна обладать матрица ![]() ?
?
· Скалярное произведение в геометрическом
пространстве ![]() .
.
Определим скалярное произведение ![]() , но если только знаем длину, и какой
угол. Что такое длина?
, но если только знаем длину, и какой
угол. Что такое длина?
3 свойство выполнено или нет – это большой вопрос.
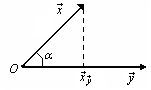
![]() , следовательно,
, следовательно, ![]() .
.
Т. к. проекция суммы есть сумма проекций:
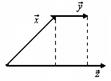 , то перед нами скалярное произведение.
, то перед нами скалярное произведение.
· Скалярное произведение в пространстве функций ![]() .
.
Определим 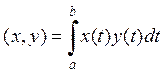 . Аксиомы
выполнены по свойствам интеграла, а значит, перед нами скалярное произведение.
. Аксиомы
выполнены по свойствам интеграла, а значит, перед нами скалярное произведение.
2. Неравенство Коши – Буняковского
Рассмотрим скалярное произведение ![]() в силу 4 свойства. Раскроем скобки,
используя свойства аддитивности и однородности:
в силу 4 свойства. Раскроем скобки,
используя свойства аддитивности и однородности: ![]() –
квадратный трехчлен относительно
–
квадратный трехчлен относительно ![]() , который
неотрицателен для
, который
неотрицателен для ![]() , следовательно,
, следовательно, ![]() .
. ![]()
или
![]() – неравенство Коши – Буняковского,
которое еще записывается в виде:
– неравенство Коши – Буняковского,
которое еще записывается в виде: ![]() .
.
Неравенство выполняется в любом линейном пространстве,
т. к. выводится только из свойств скалярного произведения. Знак равенства в том
случае, если ![]() или
или ![]() равны
равны
![]() , или
, или ![]() (
(![]() и
и ![]() одного
направления).
одного
направления).
Рассмотрим, какой вид примет данное неравенство в конкретных линейных пространствах.
· В арифметическом пространстве ![]() .
.
![]() – неравенство
Коши.
– неравенство
Коши.
· В пространстве функций ![]() .
.
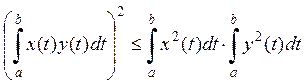 – неравенство
Буняковского (Шварца).
– неравенство
Буняковского (Шварца).
Этими неравенствами будем пользоваться и отдельно доказывать не будем, т. к. мы доказали его для любого линейного пространства.
В некоторых учебниках можно найти вывод этих неравенств отдельно для каждого пространства.
3. Норма вектора и угол между векторами
Норма элемента ![]() ,
обозначается
,
обозначается ![]() , – это функционал типа
, – это функционал типа ![]() , который удовлетворяет свойствам:
, который удовлетворяет свойствам:
1.
![]() ,
, ![]() – неотрицательность,
– неотрицательность,
2.
![]() –
однородность,
–
однородность,
3.
![]() –
неравенство Минковского (треугольника).
–
неравенство Минковского (треугольника).
Определим пока норму элемента следующим образом: ![]() . Очевидно, что свойства 1 и 2
выполняются. Проверим выполнение неравенства треугольника. По определению
. Очевидно, что свойства 1 и 2
выполняются. Проверим выполнение неравенства треугольника. По определению
![]()
![]()
![]()
![]()
![]() (второе слагаемое неположительное по неравенству Коши
– Буняковского)
(второе слагаемое неположительное по неравенству Коши
– Буняковского)![]()
![]() .
.
Норму ассоциируют как длину.
![]() Линейное пространство со скалярным
произведением называют Евклидовым. Если определена норма, то нормированным.
Линейное пространство со скалярным
произведением называют Евклидовым. Если определена норма, то нормированным.
Замечание. Норму можно ввести и другими способами, главное, чтобы она удовлетворяла свойствам нормы. Если норма появилась как следствие скалярного произведения, то норма называется евклидовой.
Упражнение. Докажите, что
норма евклидова ![]()
![]() .
Каким скалярным произведением она порождается?
.
Каким скалярным произведением она порождается?
Если
мы определим норму как ![]() , то неравенство
Коши – Буняковского примет вид:
, то неравенство
Коши – Буняковского примет вид: ![]() .
.
![]() Определим угол между
векторами
Определим угол между
векторами ![]() следующим образом
следующим образом 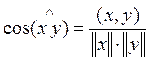 .
.
Определение
корректно, т. к. в силу неравенства Коши – Буняковского: 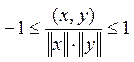 , то
, то 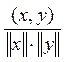 –
косинус некоторого угла.
–
косинус некоторого угла.
Тогда
![]() .
.
Примеры.
· ![]() :
: 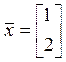 ,
, 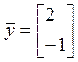 .
.
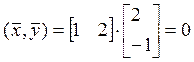 .
.
Вычислим угол: ![]() ,
, ![]() , тогда
, тогда 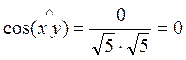 .
.
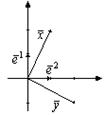 Если система координат декартова (единичные векторы
обозначаем как
Если система координат декартова (единичные векторы
обозначаем как ![]() ):
):
, то ![]()
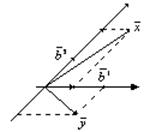 Если система координат криволинейна?
Если система координат криволинейна?
То ![]() , тогда
, тогда ![]() , где
, где ![]() –
некоторая матрица.
–
некоторая матрица.
· ![]() .
.
![]() ,
, ![]() . Найдем нормы:
. Найдем нормы: 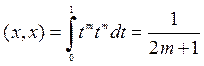 ,
, 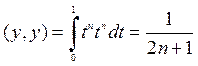 .
.
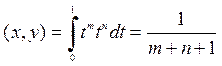 , тогда угол между функциями:
, тогда угол между функциями: 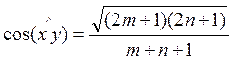 .
.
4. Ортогональность
![]() Элементы
Элементы ![]() ортогональны,
если
ортогональны,
если ![]() .
.
Т.
к. ![]() , то из определения следует что, либо
, то из определения следует что, либо
![]() , либо
, либо ![]() ,
либо
,
либо ![]() .
.
Примеры.
· ![]() .
. ![]() ,
, ![]() .
.
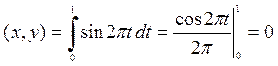 , следовательно
, следовательно ![]() .
.
Вставить рисунок
· Типовая задача 1. Вычислить все элементы ![]() ,
ортогональные
,
ортогональные ![]() .
.
![]()
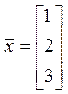 .
Обозначим
.
Обозначим  . По определению
. По определению ![]() .
. 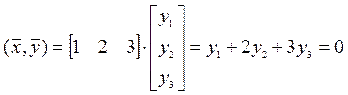 –
однородная система ранга 1.
–
однородная система ранга 1.
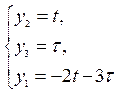 .
.
Т.
о.  . Геометрический образ – это
плоскость.
. Геометрический образ – это
плоскость.
5. Типовые задачи
· Типовая задача 2. Нормировать элемент линейного пространства.
Т.
е. представить его в виде ![]() , где
, где ![]() – единичный вектор (орт), того же
направления, что и
– единичный вектор (орт), того же
направления, что и ![]() . Вычислим норму элемента
. Вычислим норму элемента ![]() :
: ![]() (т.
к.
(т.
к. ![]() )
)![]() .,
т. е.
.,
т. е. ![]() .
.![]()
Значит,
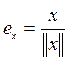 .
.
Пример. ![]()
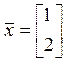 ,
,
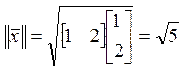 . Следовательно,
. Следовательно, 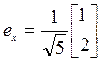 .
.
· Типовая задача 3. Вычислить
угол между элементами ![]() .
.
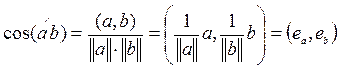 . Т. е. угол – это разница между направлениями
и от длин не зависит (как в геометрическом пространстве).
. Т. е. угол – это разница между направлениями
и от длин не зависит (как в геометрическом пространстве).
· Типовая задача 4. Вычислить
длину проекции элемента ![]() на направление
на направление
![]() .
.
![]()
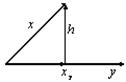 – проекция
– проекция ![]() на
на ![]() . Вектор
. Вектор ![]() –
расстояние от вектора
–
расстояние от вектора ![]() до
до ![]() . Тогда
. Тогда
![]() – коэффициенты Фурье.
– коэффициенты Фурье.
· Типовая задача 5. Вычислить
проекцию элемента ![]() на направление
на направление ![]() .
.
![]() – проекция элемента
– проекция элемента ![]() на направление
на направление ![]() . Тогда
. Тогда ![]() расстояние
от вектора
расстояние
от вектора ![]() до
до ![]() .
.
Замечание. Проекция – это вектор, длина проекции – это число.
6. Метрика линейного пространства
Пусть ![]() – линейное
пространство. Всякое линейное пространство можно задать как линейную оболочку
некоторой линейно независимой системы
– линейное
пространство. Всякое линейное пространство можно задать как линейную оболочку
некоторой линейно независимой системы ![]() :
: ![]() , тогда любой элемент линейного
пространства можно представить линейной комбинацией векторов
, тогда любой элемент линейного
пространства можно представить линейной комбинацией векторов ![]() . Пусть
. Пусть ![]() ,
,
![]() .
.
Найдем скалярное произведение:
![]() (раскроем,
используя свойства)
(раскроем,
используя свойства)
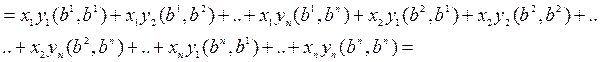
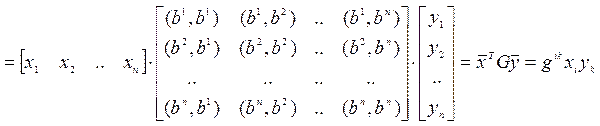 – общий случай скалярного
произведения.
– общий случай скалярного
произведения.
![]() – называется
матрицей Грама.
– называется
матрицей Грама.
![]() – это
арифметический объект. Он и называется тензором скалярного произведения или
метрическим тензором.
– это
арифметический объект. Он и называется тензором скалярного произведения или
метрическим тензором.
В тензорном виде: ![]() .
.
· Типовая задача 6. Вычислить скалярное произведение.
![]() .
.
Если
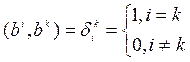 , то
, то ![]() ,
тогда
,
тогда ![]() .
.
Если
![]() , то элементы
, то элементы ![]() и
и
![]() ортогональны.
ортогональны.
Пример.
В
![]() дан метрический тензор
дан метрический тензор 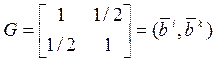 . Вычислить скалярное произведение
векторов
. Вычислить скалярное произведение
векторов 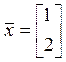 и
и 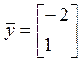
1)
в системе ![]() , 2) в системе
, 2) в системе ![]() .
.
1).
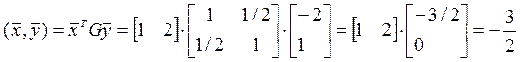 .
.
2).
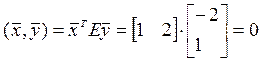 , следовательно
, следовательно ![]() .
.
Зачем нужен базис? Чтобы сопоставить векторам их координаты,
т. е. арифметику (мы умеем работать с числами). Вводя матрицу ![]() , мы навязываем арифметическому
пространству геометрию.
, мы навязываем арифметическому
пространству геометрию.
Пример. Дан базис в геометрическом пространстве:
![]() Найти метрический тензор.
Найти метрический тензор.
В
геометрическом пространстве длину угол можем замерить, если вооружимся линейкой
и транспортиром, тогда 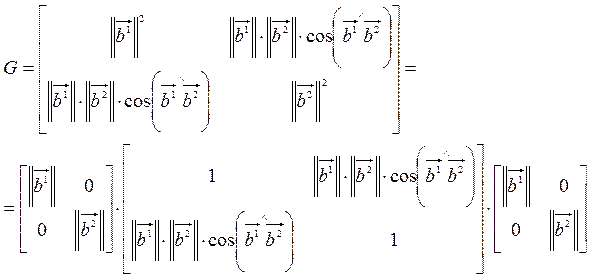
– разложение метрического тензора на нормы и углы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.