ЭВМ в технике и научных исследованиях: Учебное пособие, страница 2

Обработка прерываний является механизмом самого процессора. Прерывание осуществляется с помощью процедур обработки прерываний (ПОП), адреса которых хранятся в фиксированных ячейках. Каждый адрес ячейки связан с определенным прерыванием.

Процесс обработки прерывания изображен на рис. 2. Прерывание начинается с запроса прерывания (ЗП), который соответствует какому-либо событию. При поступлении запроса процессор сначала заканчивает команду (К_i), во время которой пришел сигнал запроса, и передает управление на процедуру обработчика прерываний (ПОП). По окончании процедуры обработки прерывания, управление передается в основную программу для выполнения следующей за К_i команды.

Процедура обработки прерывания отличается от обычной процедуры тем, что вначале запоминается состояние регистров процессора, а в конце процедуры регистры восстанавливаются. Тем самым достигается корректность выполнения программы, т.к. результаты выполнения команд процессора передаются через регистры. Кроме этого, ПОП должна быть достаточно короткой по времени выполнения, чтобы следующее прерывание приходило после завершения предыдущего прерывания.

2. Применение ЭВМ для решения задач математической физики

2.1. Постановка задачи математической физики

Задача математической физики в общем виде может быть поставлена следующим образом. Пусть задана область D  с границей  (см. рис. 3). Область D может быть n-мерной. Требуется найти такую функцию U, которая в области D+ удовлетворяла бы уравнению

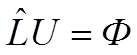  ,                                         (1)

а  на  границе  области    – условию

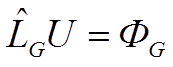 ,                                     (2)

 где  – дифференциальные или интегральные операторы, а  – известные функции.

Разные задачи математической физики имеют различные операторы . В случае задачи электростатики оператором  является оператор Лапласа, который в трехмерном случае имеет вид:

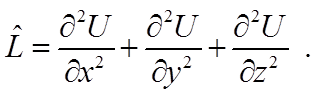                                                                                (3)

Для задачи электростатики функция правой части Ф = ρ(x,y,z)/εε₀ (уравнение Пуассона) или Ф = 0 (уравнение Лапласа).

Аналитическое решение задачи математической физики часто является очень сложной задачей, поэтому приходится прибегать к численным методам. Существуют две группы численных методов решения такой задачи:

1)  конечно-разностный;

2)  вариационный.

2.2. Конечно-разностный метод

Функция U ищется в виде сеточной функции:

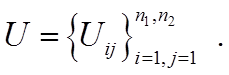                                                                                                 (4)

Такая функция задаётся набором значений , для этого область D покрывают сеткой с шагами , . В узловых значениях сетки располагаются узловые значения сеточной функции (точки на рис. 4). Таким образом, сеточная функция описывает значения на дискретном множестве точек.

Для аппроксимации значений конечноразностной функции введём понятие конечной разности.

Конечной разностью первого порядка по координате x (координате y) называется разность двух соседних узловых значений функции:

                          ,                                   (5)

Конечной разностью второго порядка называется разность конечных разностей первого порядка:

                 ,                  (6)

Разделённая разность первого порядка – это результат деления конечной разности первого порядка на шаг по соответствующей координате:

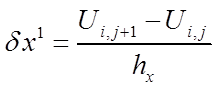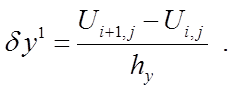                           ,                                (7)

Разделенная разность второго порядка – это конечная разность второго порядка, делённая на квадрат шага по соответствующей координате.

Разделённые разности являются численными аналогами производных, а конечные разности — дифференциалов.

В случае задачи электростатики функция U внутри области D должна удовлетворять уравнению Лапласа:

 .

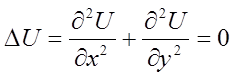 Если учесть, что численными аналогами частных производных будут являться разделённые разности, получим:

,

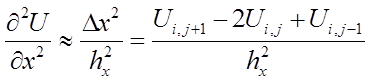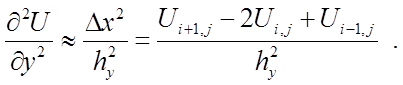
В случае, если из уравнения (3), получим:

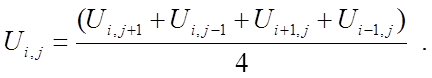                                                                (8)

конечно-разностный аналог уравнения Лапласа. Расположение точек представлено на рис. 5.

Задача свелась к системе линейных алгебраических уравнений, которую можно решить, например итерационным методом.

2.3. Вариационный метод

В основе вариационного метода лежит основное интегральное тождество.

Если  для произвольной пробной функции  имеет место основное интегральное тождество

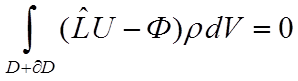                                         ,                                              (9)

то функция U является решением (9) тогда и только тогда, когда U является решением уравнений (1) и (2).

 Если вместо U в основное интегральное соотношение подставить некоторую функцию , то интеграл будет отличен от нуля: 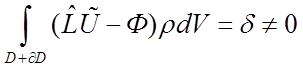, так как  не является решением соотношения (9). Величинуможно рассматривать как ошибку аппроксимации решения. Минимизируя , можно найти наилучшее решение задачи математической физики.

2.4. Кусочная аппроксимация решения  задачи математической физики

Область D можно разделить на куски , на каждом из которых строится кусок функции. Таким образом, вся поверхность кусочной функции представляет собой совокупность кусков 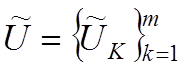 (рис. 7). Каждый из кусков 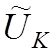 может быть построен с помощью полинома невысокой степени. Это связано с тем, что решения, полученные вариационным методом для  полиномов высокой степени, неустойчивы.

Для аппроксимации отдельных кусков часто используется поверхность Безье (двухмерный полином Бернштейна):

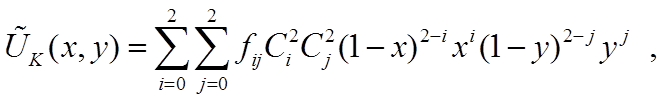                             (10)

где – узловые значения функции (в случае двумерной функции их девять для полинома 2-й степени), .  Из соотношения (10) следует, что значения полинома в углах куска совпадают с его узловыми значениями.