Другие предметы \ Системный анализ

Системный анализ и принятие решений: Методические указания к лабораторным работам, страница 6

       Iвх – исходная информация для порождения альтернатив;

       Iвых – множество порожденных альтернатив;

       Iреш – выбранная альтернатива;

       Р – правила порождения альтернатив;

       С – правило выбора наилучшей альтернативы.

1.2. Задачи оптимального выбора

Задачи оптимального выбора в общей теории системного анализа относятся к задачам исследования операций. В настоящее время под исследованием операций понимают науку, сущность которой состоит в применении научных принципов, методов и средств к задачам, связанным с функционированием систем. Эту информацию необходимо предоставить тем, кто отвечает за управление данными системами и оптимальные решения поставленных задач.

Исследование операций предполагает построение математической модели операции. Это отнюдь не означает пренебрежение натурным экспериментом. Натурные исследования обязательно должны быть проведены в той мере, которая обеспечивает построение модели и введение в модель необходимой информации.

Под оптимальным решением понимают решение (управление), минимизирующее или максимизирующее некоторый критерий (целевую функцию, функцию качества) при заданной системе ограничений. Критерий  К - это некоторая функция (функционал) от принятого решения, которая позволяет количественно оценить целесообразность принятого решения.

Методологически исследование операций можно разделить на следующие этапы: составление математической модели операции, выбор критерия операции, определение информации, необходимой для исследования модели, и исследование математической задачи для отыскания оптимального решения, обеспечивающего минимальные потери материального, морального и других видов.

1.2.1. Задача оптимального размера заказа

При производстве изделий, например медицинской техники, необходимо большое количество комплектующих изделий. Эти изделия можно приобрести сразу на весь период производства (год). При этом запас изделий нужно хранить, т.е. затрачивать средства на складские помещения и обслуживающий персонал. Затраты на хранение изделий известны. Наиболее целесообразно заказывать комплектующие изделия партиями, и по мере их расходования в процессе производства заказывать новые партии изделий. В этом случае необходимо найти оптимальный размер заказа комплектующих изделий при минимальных затратах на их хранение.

При построении математической модели затрат на хранение комплектующих изделий предположим, что расходуются они по линейному закону в некоторый промежуток времени (месяц, квартал). Введем обозначения:

D – ежегодный спрос на заказ;

С0 – стоимость подачи одного заказа;

CE – стоимость хранения единицы комплектующих изделий в год;

q – объем заказа (един/заказ).

Ежегодное количество заказов можно определить как N=D/q.  Стоимость подачи заказов в год определится как S=С0(D/q). Средний размер запаса комплектующих изделий при линейном их расходовании можно определить как q/2. В этом случае найдем ежегодную стоимость хранения комплектующих изделий  SK = CE(q/2).

Общую стоимость хранения запаса комплектующих изделий можно найти как

                                  V = С0(D/q) + CE(q/2) .                                              (1)

Для определения оптимального размера заказа q необходимо найти оптимум функции V по известным правилам:

         ,                                  ,      

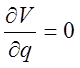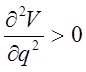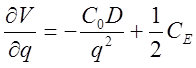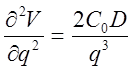 ,                 > 0  при  q > 0  ,

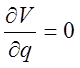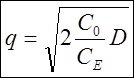    ,               ,            .                              (2)

Таким образом, по формуле (2) можно определить оптимальный размер заказа комплектующих изделий при известных параметрах производства и затратах на хранение этих комплектующих изделий.

1.2.2. Задача по замене оборудования

В последнее время в медицине применяются все более сложные и дорогостоящие приборы и оборудование. Такое оборудование иногда требует весьма больших расходов на поддержание его в рабочем состоянии. Наряду с этим происходит разработка и выпуск современных приборов, поэтому возникает вопрос, когда следует менять оборудование на более современное.

С другой стороны, при производстве медицинской аппаратуры ее необходимо рассчитывать на примерно такой же срок эксплуатации, чтобы не вкладывать лишние средства в производство.

Различают срок службы физический ТФ и срок службы экономический ТЭ. Экономический срок службы соответствует сроку службы оборудования с минимальными затратами на его эксплуатацию. Рациональный срок службы лежит между ТФ  и ТЭ .

Стоимость эксплуатации оборудования определяется формулой

 ,

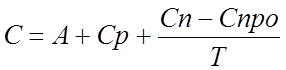где Сп – стоимость покупки;

      Спро – стоимость продажи;

      Ср – стоимость расходов на техобслуживание.

Обычно считают, что стоимость расходов на техобслуживание оборудования изменяется по линейному закону Ср=a + bТ . Коэффициенты a и b зависят от типа оборудования. С учетом средней величины расходов за период Т среднюю стоимость эксплуатации можно найти как

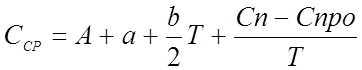                                   .                                    (3)

Из условия 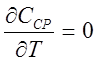 окончательно получим

                                                                                  (4)

Понятие морального старения эта формула не учитывает. Однако следует иметь в виду, что с течением времени стоимость выпускаемого оборудования уменьшается по закону Спр = Спро – kT2 . Это приводит к дополнительной потере стоимости эксплуатируемого устройства, которая за время T составляет  kT2 . С учетом этого формула (3) примет вид

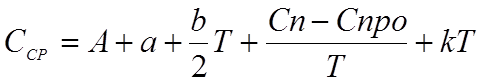                 .                               (5)

Отсюда

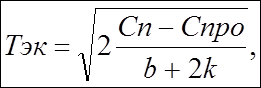                                                                                          (6)

т.е. меньше, чем в предыдущем случае.

2.  Выполнение работы

1. В первой части лабораторной работы необходимо, используя программу MathCad, решить задачу об оптимальном размере заказа комплектующих изделий при выпуске оборудования по данным табл. 1.

Скачать файл