Системный анализ и принятие решений: Методические указания к лабораторным работам, страница 4

Как правило, сложная система подвергается воздействию случайных неуправляемых факторов и других возмущающих воздействий различной природы. В результате этого изменение выходной величины Y носит случайный характер. Поэтому при построении модели системы установить точную связь между его входами и выходами не представляется возможным, и задача сводится к отысканию поверхности отклика, характеризуемой зависимостью среднего значения выходного показателя Y от входных факторов, т.е. уравнения регрессии. При этом коэффициенты полинома, определяемые по экспериментальным данным, являются статистическими оценками соответствующих истинных значений.

Полный факторный эксперимент (ПФЭ) является активным экспериментом и применяется для  отыскания математического описания объекта в виде неполной квадратичной модели. Например, для двухфакторного объекта модель такого типа имеет вид:

Y = B₀ + B₁ X₁ + B₂ X₂  + B₁₂ X₁ X₂ .                                 (2)

В эксперименте выбирается точка режима X₀ = (X₁₀, X₂₀, ... , X_n0 ) и реализуются все возможные неповторяющиеся комбинации значений факторов X_i , каждый из которых варьируется на двух граничных условиях X_{i min}, X_imax, отличающихся от базового значения на величину шага варьирования DX_i:

X_{i min}  = X_i0  - DX_i ,                                                 (3)

        X_{i max}  = X_i0 + DX_i  .                                                                  

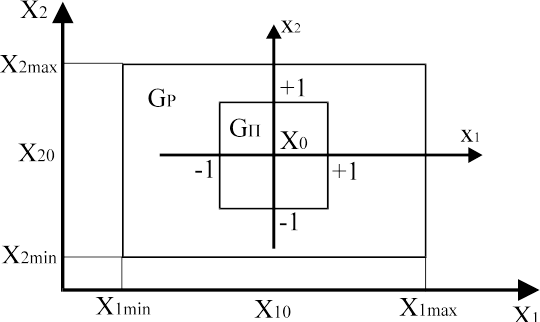
При использовании метода ПФЭ осуществляют преобразование независимых переменных X_i   к безразмерным переменным x_i  по правилу

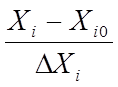                                   x_i  =  ,      i = 1, 2, ... , n .                                    (4)

В этом случае верхним и нижним уровням планирования X_{i max}  и X_{i min}  будут соответствовать значения безразмерных переменных

x_{i max}  = +1 ,   x_{i min}  = -1 ,                    i = 1,2, ... , n .

Преобразование переменных (4) соответствует переходу от области G_р  реальных значений факторов  X_i  , задаваемых неравенствами (1), к области G_п  планирования в пространстве безразмерных переменных  x_i. Геометрический смысл этого преобразования  иллюстрируется на рисунке   для случая n= 2.

При этом следует иметь в виду, что математической модели (2) в об

ласти безразмерных переменных будет соответствовать другое уравнение:

y = B₀  + B₁ x_i  + B₂ x₂  + B₁₂ x₁ x₂ .               (5)

Построение модели объекта методом ПФЭ происходит поэтапно в определенной последовательности:

а) планирование эксперимента;

б) проведение эксперимента;

в) расчет коэффициентов модели;

г) проверка статистической значимости коэффициентов модели;

д) проверка адекватности математической модели.

Этап планирования эксперимента заключается в составлении матрицы планирования эксперимента. Например, матрица планирования ПФЭ типа 2², который проводят для исследования двухфакторного объекта, имеет следующий вид:

N опыта ( l )	x1	x2	x1 x2
1	-1	-1	+1
2	+1	-1	-1
3	-1	+1	-1
4	+1	+1	+1

При проведении эксперимента  на входе объекта устанавливаются уровни факторов x_i , определяемые соответствующей строкой матрицы планирования. Для устранения ошибки эксперимента, вызванной случайными изменениями  y , в каждой точке факторного пространства проводится  m параллельных опытов и результаты наблюдений усредняются:

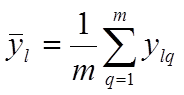                          ,   i = 1,2, ... , N   ,                                 (6)

где  y_lq  - наблюдаемое значение выхода при выполнении  l-го опыта в  q-й серии опытов.

При этом эксперименты делятся на серии опытов, в каждом из которых полностью реализуется матрица планирования. Для исключения возможных систематических ошибок в каждой серии порядок проведения опытов устанавливается случайным образом с помощью какого-либо механизма случайного выбора.

Расчет коэффициентов модели.  Метод полнофакторного эксперимента в силу ортогональности матрицы планирования позволяет получить раздельные оценки коэффициентов полиноминальной модели. В случае двухфакторного объекта оценки коэффициентов модели (5) рассчитываются по формулам:

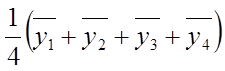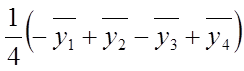B₀=  ;                B₁=  ;          (7)

B₂= 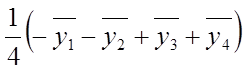 ;             B₁₂=  .

Проверка значимости оценок коэффициентов означает проверку гипотез  B_j =0 с помощью выборочного распределения Стьюдента. С этой целью для каждого коэффициента модели рассчитывается   t-статистика:

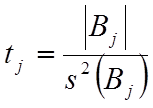                                    ,                                                        (8)

где 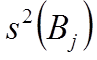  - оценка дисперсии ошибки определения коэффициентов:

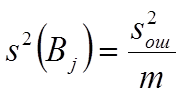                                     .                                                           (9)

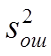В формуле (9)  величина  представляет собой оценку дисперсии  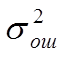ошибки эксперимента:

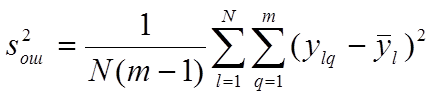                                    .                        (10)

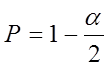Если расчетная величина   превышает значение  , определенное по таблице распределения Стьюдента для числа степеней свободы  и заданной доверительной вероятности  ,  то проверяемая гипотеза отклоняется, и коэффициент B_j  признается значимым. В противном случае  гипотеза принимается и соответствующий коэффициент считается незначимым.

В силу того, что оценки коэффициентов получены раздельно, незначимые коэффициенты могут быть отброшены без пересчета остальных. После этого в записи математической модели объекта оставляют члены, включающие только значимые коэффициенты.

Проверка адекватности (пригодности) математической модели  заключается в проверке гипотезы адекватности с использованием  F-критерия Фишера. Для этого рассчитывается оценка  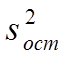 остаточной дисперсии  , характеризующей рассеяние результатов эксперимента относительно модели, аппроксимирующей искомую функцию отклика:

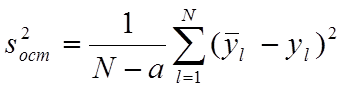            ,                             (11)

где y_i- значение выходной переменной, рассчитанное при подстановке в полученное выше уравнение  регрессии координат экспериментальной точки в относительных единицах, соответсвующей  l-му опыту;  - число значимых коэффициентов в уравнении регрессии.