Системный анализ и принятие решений: Методические указания к лабораторным работам, страница 5

Проверка адекватности модели состоит в выяснении соотношения между остаточной дисперсией и дисперсией ошибки эксперимента. Если , то полученная математическая модель адекватно представляет результаты эксперимента. В противном случае полученное описание считается неадекватным объекту.

Для проверки гипотезы о том, что 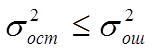  необходимо рассчитать значение F–статистики:

F= 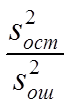  , если  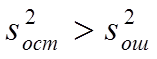         и   F = 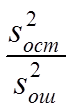  - в противном случае.

При этом следует иметь в виду, что число степеней свободы

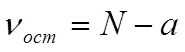                             и   .

Расчетная величина  F сравнивается при выбранной доверительной вероятности    с критическим значением  F_кр , найденным по таблицам распределения Фишера. Проверяемая гипотеза принимается, если  F< F_кр , в противном случае гипотеза отклоняется и модель признается неадекватной объекту.

В случае принятия гипотезы адекватности делается переход к модели объекта вида (2) в натуральных величинах входных переменных.  Для этого в полученном уравнении регрессии вида (5) производится подстановка переменных (4) и приведение подобных членов (при этом учитываются только значимые коэффициенты):

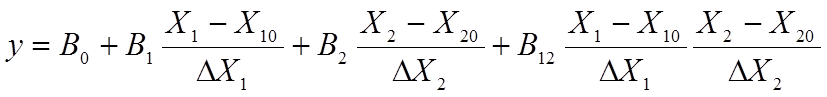 (12)

2. Описание исследуемой модели

В лабораторной работе исследуется математическая модель задания рабочей точки усилительного каскада на биполярном транзисторе. Напряжение на коллекторном выводе транзистора такого каскада задается выражением:

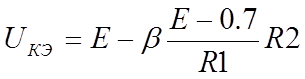                                   .                                            (13)

Необходимо, изменяя параметры резисторов R1 и R2 при заданных остальных неизменных величинах, провести эксперимент на двухфакторном объекте с применением математического пакета программ MathCad. Моделирование случайных изменений параметров резисторов задается специальной функцией программы. В каждой точке факторного пространства проводятся четыре различных опыта.

3. Порядок выполнения работы

1. Получить у преподавателя неизменные параметры выражения (15) для проведения эксперимента. Отклонения номиналов резисторов не более 10 %.

2. Завести в программу MathCad необходимые данные и сформировать нужные вычисления. Работа проводится в два этапа.

Первый этап работы заканчивается расчетом коэффициентов модели.

На втором этапе проверяется статистическая значимость коэффициентов и адекватность модели.

4. Содержание отчета

1. Краткие теоретические сведения о методе  планирования эксперимента.

2. Основные расчетные формулы и соотношения.

3. Результаты расчетов.

4. Выводы по работе

5. Контрольные вопросы

1. Назовите основные этапы формирования системы управления.

2. Охарактеризуйте этапы идентификации модели, синтеза управления, реализации управления и адаптации.

3. Охарактеризуйте этапы формирования целей, определения объекта и структурный синтез модели.

4. В чем заключается задача наблюдения за объектом?

5. В чем заключается задача классификации?

6. В чем заключается задача идентификации?

7. Что такое «критерий превосходства» при количественной оценки различных систем?

8. Что такое «функция полезности» для разных альтернатив?

Лабораторная работа № 3

Решение задачи оптимального выбора при принятии решений

Цель работы: научиться находить оптимальное решение для систем, имеющих строгое формальное описание функционирования.

1.  Краткие теоретические сведения

В жизни любой человек сталкивается с ситуацией, когда он вынужден принимать какое-то решение. Иногда это решение принимается почти интуитивно, а иногда - после оценки ситуации и окружающей обстановки. И в том и в другом случае, решая задачу о принятии правильного решения, человек пытается выйти из ситуации с наименьшими для себя потерями (моральными, материальными и др.).

При управлении сложными системами принятие тех или иных решений во многом определяет правильность и надежность функционирования системы в целом и достижения ею назначенной цели. Принятие решений для управления каждой конкретной системой весьма индивидуально, однако можно отыскать общие формальные принципы принятия решений при управлении системами различных типов.

1.1.  Модель общей задачи принятия решений (ОЗПР).

Принятие решения – это функция преобразования информации для получения максимальной выгоды. Рассмотрим центральные понятия в ОЗПР.

W - множество вариантов, альтернатив и планов для выбора.

Х – альтернативы для выбора из W (Х Í W).

Y – выбранные альтернативы (Y Î Х).

С – принцип выбора (функция выбора) – это правило по которому выбирается лучшая альтернатива (Y = С(Х)).

Механизм выбора М той или иной альтернативы зависит от многих факторов, однако его  можно легко формализовать, используя следующую запись:  М ® < d, p >,

гдеd- совокупность сведений, которые позволяют сопоставить альтернативы для оптимального выбора;

p- правила выбора. Это формализованная инструкция о том, как из Х выбрать Y .

Множество существующих задач о принятии решений после анализа можно свести к трем основным типам.

1.  Задача оптимального выбора.  В задачах этого типа W,  т.е. множество альтернатив и планов для выбора, однозначно определены. Функция выбора С  строго формализована, и оптимальное решение находят путем оптимизации заданной функции.

2.  Задачи выбора. В задачах этого типа W,   т.е. множество альтернатив и планов для выбора, также однозначно определены. Однако функция выбора С не формализована. При решении таких задач применяют экспертные оценки, теорию полезности. Решение в этом случае не всегда оптимально, но может быть рационально.

3.  Общая задача принятия решения. В задачах этого типа W, т.е. множество альтернатив и планов для выбора, заранее не известно и могут добавляться и изменяться. Функция выбора С строго не формализована. В этом случае лицо, принимающее решение (ЛПР), может изменить свое решение в случае получения дополнительной, ранее не известной информации.

Формально общая задача принятия решения (ОЗПР) может быть представлена зависящей от разных факторов:

ОЗПР ® <Т, I_вх , I_вых , Р, С, I_реш >,

где Т – цель принятия решения (выбор альтернатив или их множества);