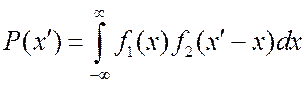Рентгенографическое исследование фибриллярных структур. Рентгендифракционные исследования мышц (Разделы 3-4 учебного пособия "Рентгенография биологических объектов"), страница 3

                                   .                            (3.29)

Если одна из функций обладает центром инверсии, то .

Используя свертывание функций, структуру цепочечной молекулы можно представить как результат распределения некоторой атомной группировки по узлам одномерной линейной решетки, то есть использовать -свертку соответствующих функций. Напишем интеграл Фурье от -свертки

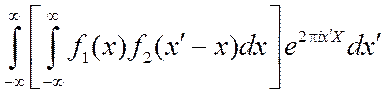                                 .                   (3.30)

После замены  выражение (3.30) можно преобразовать следующим образом

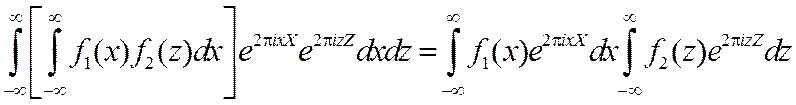 , (3.31)

то есть оно равно произведению трансформант Фурье функций  и . Следовательно, трансформанта Фурье свертки двух функций равна произведению трансформант этих функций.

Аналогичным образом можно показать, что справедливо и обратное утверждение: интеграл Фурье от произведения двух функций равен свертке интегралов Фурье каждой из них:

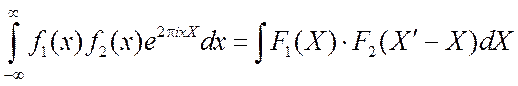                   ,              (3.32)

где  и  – трансформанты Фурье функций  и . Таким образом, мы сформулировали теорему свертки. Можно отметить, что представленные выражения справедливы и для трехмерного случая.

Так как трансформанты периодических функций отличны от нуля только при целых величинах 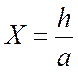, то, если  и  имеют период , вместо интегралов Фурье  используют ряды Фурье.

Если получить -свертку функции с самой собою, то результатом является «самосвертка» или «квадратичная свертка». Самосвертка электронной плотности  (трехмерный случай) имеет вид

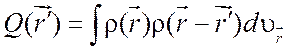                                                                  (3.33)

и называется функцией межатомных расстояний или функцией Паттерсона, которая была ранее определена при рассмотрении дифракции на кристаллах.

В качестве примера применения теоремы свертки снова обратимся к дифракции на непрерывной спирали. На рис. 3.11 дано схематическое представление непрерывной спирали и дифракционной картины от нее, полученное путем применения понятия свертки двух функций.

Теперь рассмотрим дифракцию на прерывных спиральных структурах. Основными характеристиками такой спирали являются: период непрерывной спирали , шаг спирали  (т.е. проекция на ось спирали расстояния между соседними субъединицами) и истинный период прерывной спирали  (рис. 3.12).

Рис. 3.11. Схема представления непрерывной спирали (в)

как свертки одного оборота спирали (а) с рядом точек, расположенных вдоль оси спирали на расстояниях Р друг от друга (б). Дифракционная картина такой спирали (е) является произведением дифракционных

картин от одного оборота спирали (г) и ряда точек (д)

Рис. 3.12. Прерывная спиральная структура:

а – целочисленная спираль (5 субъединиц на оборот);

б – нецелочисленная спираль (7 субъединиц на оборот)

Выделяют целочисленные спирали, когда на один оборот спирали приходится  субъединиц. Тогда, если , то 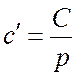, а период непрерывной спирали  равен периоду прерывной спирали  (рис. 3.12, а). В другом случае  субъединиц приходится на  оборотов 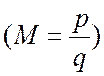 и спираль называется нецелочисленной. Для такой спирали истинным периодом, то есть расстоянием между трансляционно идентичными субъединицами, будет величина , определяемая соотношениями

                         .                             (3.34)

Этот период больше периода непрерывной спирали в  раз (рис. 3.12, б). В качестве примера приведем -спираль, которая характерна для фибриллярных белков и определяется следующими параметрами: С=5,4 Å, с¢=1,5 Å, с=27 Å. Поэтому -спирали соответствует величина 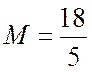, и эта структура содержит 18 субъединиц в 5 оборотах.

Прерывную спираль можно представить как произведение непрерывной спирали и набора параллельных плоскостей, расстояние между которыми равно  (шаг спирали) (рис. 3.13). По теореме свертки дифракционная картина прерывной спирали является сверткой дифракционных картин непрерывной спирали и набора параллельных плоскостей. Трансформанта Фурье такого набора представляет ряд точек на меридиане, отстоящих друг от друга на расстояние . Поэтому дифракционная картина состоит из серии «крестов», помещенных в точки меридиана рентгенограммы (меридиан – вертикальная ось рентгенограммы, проходящая через ее центр – первичный пучок), имеющие расстояние m/c¢  от центра рентгенограммы (рассматриваем дифракцию от целочисленной прерывной спирали). Таким образом, это будут слоевые линии, но расположенные чаще, чем для непрерывной спирали, а распределение интенсивности на каждой слоевой будет определяться не одной, а несколькими функциями Бесселя (рис. 3.13). Поэтому в этом случае появляются рефлексы на меридиане, а при  такой рефлекс определяет величину проекции расстояния между субъединицами на ось спирали.

Рис. 3.13. Схема образования дифракционной картины (е)

от прерывной спирали (в) как свертки дифракционных картин (г, д)

от непрерывной спирали (а) набора плоскостей (б)

В случае нецелочисленной прерывной спирали образование дифракционной картины более сложно, хотя принцип ее построения аналогичен рассмотренному выше (рис. 3.14). Положения слоевых линий, даваемых такой спиралью, могут быть определены следующим образом:

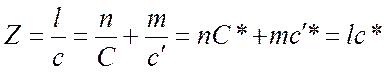                             ,                       (3.35) где величины  и  могут принимать значения . Если отношение  рационально, то индекс  системы слоевых линий определяется по соотношению

                                          ,                                              (3.36)

а расстояние между слоевыми линиями в этом случае равно

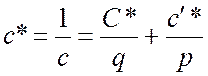                                      .                                       (3.37)

Рис. 3.14. Схема дифракционной картины (б)

от целочисленной спирали 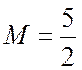 периода R (а)

Выражение (3.36) называется правилом отбора и позволяет определить целочисленные индексы  за счет изменения . В результате для нецелочисленной прерывной спирали вместо соотношения (3.27) следует использовать выражение

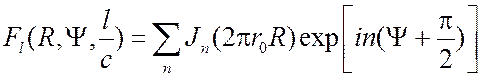                  ,                    (3.38)