Не рассматривая все указанные модели, в качестве примера приведем
задачу о рассеянии сплошным цилиндром радиусом ![]() ,
плотность которого задается следующим образом:
,
плотность которого задается следующим образом:
 (3.18)
(3.18)
Из-за цилиндрической симметрии в выражении (3.16) все члены с
![]() будут равны нулю. Поэтому, используя
(3.16) или (3.10), получаем
будут равны нулю. Поэтому, используя
(3.16) или (3.10), получаем
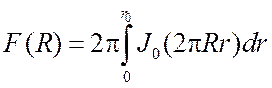 .
(3.19)
.
(3.19)
Так как между функциями Бесселя имеются соотношения
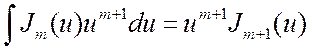 ,
(3.20)
,
(3.20)
то
![]() ,
(3.21)
,
(3.21)
где ![]() .
.
|
|
Графическое представление функции ![]() приведено
на рис. 3.5. Первый нуль этой функции имеет место при
приведено
на рис. 3.5. Первый нуль этой функции имеет место при ![]() ,
что соответствует
,
что соответствует 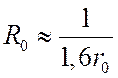 . Таким образом, чем меньше
радиус цилиндра
. Таким образом, чем меньше
радиус цилиндра ![]() , тем шире его
трансформанта Фурье
, тем шире его
трансформанта Фурье ![]() , если ширину
характеризовать положением первого максимума функции
, если ширину
характеризовать положением первого максимума функции ![]() .
Если
.
Если ![]() , то цилиндр становится сплошной
прямой. В этом случае положение первого нуля передвигается в бесконечность, то
есть
, то цилиндр становится сплошной
прямой. В этом случае положение первого нуля передвигается в бесконечность, то
есть ![]() , и получается рассеяние бесконечно
протяженной прямой в цилиндрических координатах. Поэтому одномерная дифракция
от объектов типа линии имеет своим образом плоскость в обратном пространстве
(рис. 3.6, б). Можно добавить, с другой стороны, что двумерная дифракция от
объектов, представляющих плоскости, имеет своим образом в обратном пространстве
сплошные линии (рис. 3.6, а).
, и получается рассеяние бесконечно
протяженной прямой в цилиндрических координатах. Поэтому одномерная дифракция
от объектов типа линии имеет своим образом плоскость в обратном пространстве
(рис. 3.6, б). Можно добавить, с другой стороны, что двумерная дифракция от
объектов, представляющих плоскости, имеет своим образом в обратном пространстве
сплошные линии (рис. 3.6, а).
Рис. 3.5. График функции ![]()
|
|
Рис. 3.6. Трансформанты Фурье плоскости (а)
и прямой линии (б) бесконечной протяженности
Вообще существует общее правило, по которому размеры («полуширины») трансформант в одинаковых направлениях обратны друг другу, а их произведение равно единице.
Соотношение
(3.21) дает трансформанту Фурье для цилиндра бесконечной длины. Если
рассеивающий объект имеет конечную длину ![]() ,
то для получения окончательного результата это соотношение нужно еще умножить
на величину, дающую зависимость от
,
то для получения окончательного результата это соотношение нужно еще умножить
на величину, дающую зависимость от ![]() :
:
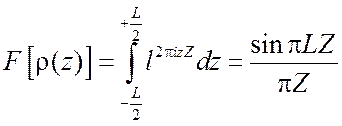 . (3.22)
. (3.22)
Теперь
обратимся к рассмотрению дифракции на спиральных структурах, которые
присутствуют во многих биологических объектах и играют важную роль в физике
биополимеров. Такая спиральная конфигурация часто встречается в цепочечных
молекулах. Наиболее удобно описывать спиральные структуры в цилиндрических
координатах. Поэтому можно использовать ранее приведенные общие формулы. При
рассмотрении выделяют непрерывные и прерывные спирали. Сначала обратимся к
непрерывной спирали. Ее можно охарактеризовать периодом ![]() и
радиусом
и
радиусом ![]() (рис. 3.7). Пусть при
(рис. 3.7). Пусть при ![]() . Тогда при
. Тогда при ![]() .
Поэтому уравнение спирали в цилиндрических координатах имеет вид
.
Поэтому уравнение спирали в цилиндрических координатах имеет вид
|
|
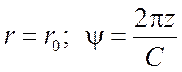 .
(3.23)
.
(3.23)
Рис. 3.7. Схема непрерывной спирали
Для спиральной структуры с периодичностью вдоль оси z интеграл (3.7) перепишется в виде
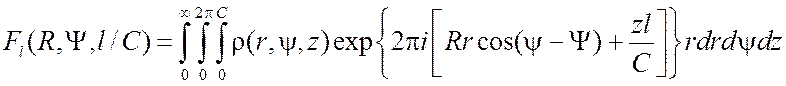 , (3.24)
, (3.24)
где ![]() – распределение плотности в
повторяющейся элементарной группе, а интегрирование по координате
– распределение плотности в
повторяющейся элементарной группе, а интегрирование по координате ![]() осуществляется в пределах одного периода
осуществляется в пределах одного периода
![]() .
.
Если
принять плотность ![]() вдоль оси спирали равной
единице, то для непрерывной спирали ее можно представить как произведение двух
вдоль оси спирали равной
единице, то для непрерывной спирали ее можно представить как произведение двух ![]() -функций
-функций
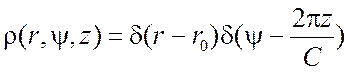 . (3.25)
. (3.25)
Тогда для трансформанты Фурье (3.24) с учетом (3.23) и (3.25) получается выражение
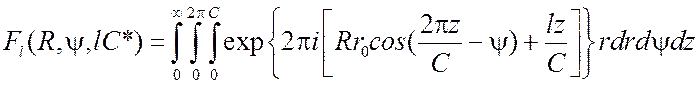 . (3.26)
. (3.26)
Далее, используя (3.9), можно выразить трансформанты через функции Бесселя
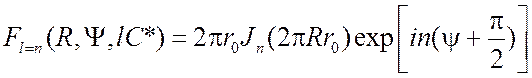 , (3.27)
, (3.27)
где ![]() – функция Бесселя
– функция Бесселя ![]() -го порядка. Следует отметить, что модуль
выражения (3.27) равен
-го порядка. Следует отметить, что модуль
выражения (3.27) равен ![]() и имеет
цилиндрическую симметрию, а распределение интенсивности на слоевой линии с
номером
и имеет
цилиндрическую симметрию, а распределение интенсивности на слоевой линии с
номером ![]() определяется квадратом функции
Бесселя
определяется квадратом функции
Бесселя ![]() -го порядка. Как было отмечено ранее,
расстояние от начала координат первого максимума бесселевых функций
увеличивается с увеличением
-го порядка. Как было отмечено ранее,
расстояние от начала координат первого максимума бесселевых функций
увеличивается с увеличением ![]() (рис. 3.4).
Поэтому распределение интенсивности по слоевым линиям имеет характерный вид
«креста» (рис. 3.8, а). Объяснение крестообразного вида распределения
интенсивностей может быть также дано на основе ранее сделанного утверждения о
том, что структурный фактор
(рис. 3.4).
Поэтому распределение интенсивности по слоевым линиям имеет характерный вид
«креста» (рис. 3.8, а). Объяснение крестообразного вида распределения
интенсивностей может быть также дано на основе ранее сделанного утверждения о
том, что структурный фактор ![]() имеет наибольшее
значение, когда вектор
имеет наибольшее
значение, когда вектор ![]() перпендикулярен к ряду,
наиболее плотно «заселенному» атомами. На рис. 3.8, б представлены «густо заселенные»
ряды спиральной структуры и проведенные к ним нормали вектора
перпендикулярен к ряду,
наиболее плотно «заселенному» атомами. На рис. 3.8, б представлены «густо заселенные»
ряды спиральной структуры и проведенные к ним нормали вектора ![]() , которые образуют крест.
, которые образуют крест.
|
|
Рис. 3.8. Графики функций Бесселя ![]() для различных значений l (а)
для различных значений l (а)
и схема крестообразного расположения нормалей к наиболее плотно
«заселенным» рядам спирали, объясняющая характерное распределение
интенсивностей на слоевых линиях рентгенограммы (б)
Наиболее четко картина косого креста наблюдается на рентгенограммах, полученных от образцов спиральных структур, не имеющих кристаллической упорядоченности (рис. 3.9), когда нет межмолекулярного рассеяния и дифракционная картина обусловлена внутримолекулярным рассеянием. Чем более упорядоченно расположены молекулы в образце, тем большую роль имеют эффекты межмолекулярного рассеяния и суммарная картина уже не выявляет наличие «косого креста» в чистом виде (рис. 3.10).
При интерпретации дифракционных картин от спиральных структур
широко используют операцию свертывания функций. Под сверткой понимают
распределение одной функции ![]() по закону,
задаваемому другой функцией
по закону,
задаваемому другой функцией ![]() :
:
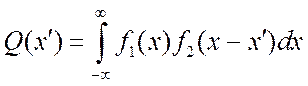 .
(3.28)
.
(3.28)
|
|
Рис. 3.9. Рентгенограмма ориентированного геля спиральных молекул
(натриевая соль ДНК во влажном состоянии)
|
|
Рис. 3.10. Рентгенограмма текстуры натриевой соли ДНК
в кристаллической форме А
Выражение
(3.28) представляет так называемую ![]() -свертку, дающую
распределение функции
-свертку, дающую
распределение функции ![]() по закону, задаваемому
второй функцией
по закону, задаваемому
второй функцией ![]() , которая инвертирована
относительно пространства свертки. Чтобы получить распределение одной функции
по закону, задаваемому другой без инвертирования в пространстве свертки, надо
использовать
, которая инвертирована
относительно пространства свертки. Чтобы получить распределение одной функции
по закону, задаваемому другой без инвертирования в пространстве свертки, надо
использовать ![]() -свертку
-свертку
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.