Для входного участка коэффициент трения
ζвх = 0,5(1 – Fк/F’)0,75. (77)
Для выходного участка
ζвых = (F’/Fк – 1)2. (78)
В этих формулах F’ = (π/4)[(Dан + 2tр)2 – Dан2] – площадь патрубка воздуховода.
В канале охлаждения
Δpк = ζкhрv2g /(2dэф). (79)
Коэффициент ζк = 64/Re при ламинарном и ζк = 0,316/Re0,25 при турбулентном режимах движения.
После проверки условий работы вентилятора рассчитывается по формуле (70) критерий Нуссельта Nu, а затем – коэффициент теплоотдачи
a = Nu×l/dэф.
Заключительным этапом проектирования является расчет максимальной температуры ребер Tрм и максимальной температуры анода Tам.
Тепловой баланс элементарного участка по длине ребра протяженностью dx описывается соотношением
Qx – Qx+dx =2ahр(T – T0)dx.
В соответствии с уравнением Фурье
Qx = –lрhрdр(dT/dx)x;
Qx+dx = –lрhрdр(dT/dx)x+dx = –lрhрdр[(dT/dx)x + (d2T/dx2)dx],
где lр– коэффициент теплопроводности материала ребра.
Из условий теплового баланса на элементарном участке по длине ребра следует:
d2T/dx2 = 2[a/(lрdр)] (T – T0). (80)
Полагаем, что на аноде выделяется мощность электронной бомбардировки Pa и вся мощность, излучаемая катодом Pf. Часть мощности рассеивается в просвете между ребрами, остальная – отводится ребрами системы охлаждения. Теплоотводом в окружающее пространство с торцов концевых участков можно пренебречь (рис. 22,б). В результате граничные условия уравнения (80) принимают вид:
при x = 0 dT/dx = [(Pa +Pf) – npbрhрa(Tpm – T0)] /(nplр hрdр);
при x = tр dT/dx = 0.
После интегрирования получаем формулу для расчета максимальной температуры ребер:
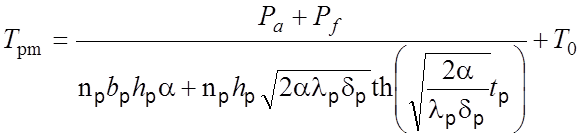. (81)
Температура внутренней стенки анода
Tам = Tрм+ (Pa +Pf)Dа/(la2prаhр), (82)
lа – коэффициент теплопроводности материала анода.
Найденные значения максимальной температуры анода и ребер определяют работоспособность выбранного варианта системы охлаждения.
Во избежание заметного испарения в вакууме и разрушения спая стекла с металлом температура внутренней поверхности анода не должна превышать 300 0С.
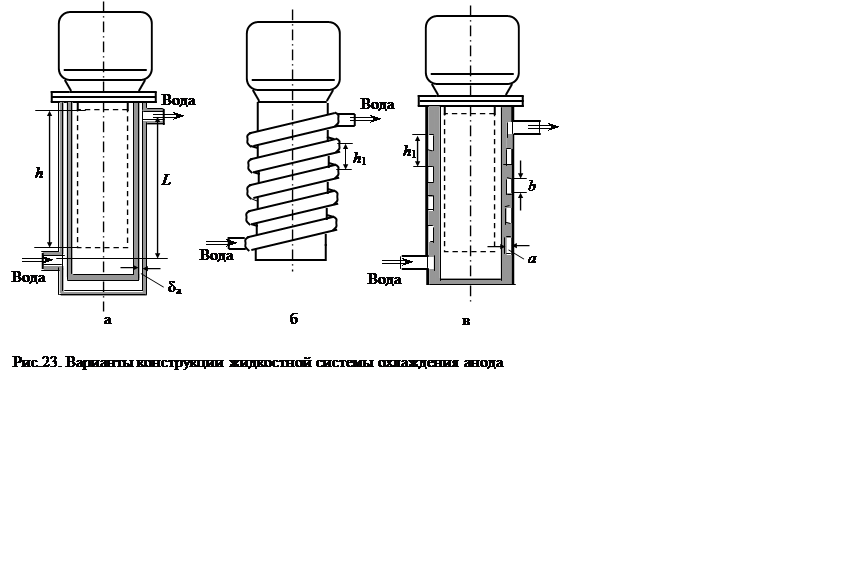
Жидкостное охлаждение по сравнению с воздушным обладает заметно более высокой эффективностью, обеспечивая аналогичный теплоотвод при меньших рабочих температурах. В качестве теплоносителя могут быть различные жидкости, но чаще всего используется вода. Водяное охлаждение характеризуется наиболее высокой эффективностью благодаря рекордной теплоемкости воды и достаточно высокой ее теплопроводности. Недостатком жидкостного охлаждения является сложность реализации на подвижных объектах.
Наиболее простым вариантом жидкостного охлаждения является система в виде рубашки охлаждения (рис.23,а). Однако при больших поперечных размерах анода работа такой системы сопровождается повышенным расходом жидкости. Более экономичной считается система в виде змеевика из медной трубки, напаиваемой на внешнюю сторону анода (рис.23,б), либо система в виде спиральной проточки (рис.23,в). Недостатком последних двух вариантов является большое гидродинамическое сопротивление, оказываемое жидкостному потоку.
В качестве исходных величин для системы в виде рубашки охлаждения выбираются зазор dа и протяженность канала охлаждения L. Для системы в виде змеевика – внутренний диаметр медной трубки d и шаг намотки h1. Для системы в виде спиральной проточки – шаг спирали h1, глубина a и ширина проточки b.
Задавшись толщиной стенок анода Dа, определяют наружный диаметр анодного цилиндра
Dан = 2(ra+Dа). (83)
Для выбранного варианта рассчитывают эффективный диаметр dэф, площадь поперечного сечения Fк, длину канала охлаждения L0 и площадь охлаждаемой поверхности анода Fа0.
Для системы в виде рубашки охлаждения
dэф= 2dа, Fk= (p/4)[(Dан+2dа)2–Dан2], L0=L, Fa0 = pDанh.
 |
dэф = d, Fk= pd2/4,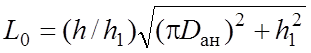 
, Fa0 = (pdL0)/2.
Для системы в виде спирали
dэф=2ab/(a+b),
Fk=ab, 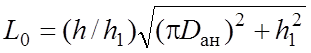, Fa0 = L0(2a+b).
Для подачи воды чаще всего применяют водопроводную сеть. Производительность водопроводной сети примерно 15...18 л/мин. Если такая производительность оказывается недостаточной, применяют замкнутые системы с подачей воды специальными насосами и охлаждением воды в градирнях либо брызгательных бассейнах. Производительность может составлять 30, 50, 100 л/мин.
При использовании системы в виде змеевика либо спиральной проточки производительность падает из-за большого гидродинамического сопротивления канала. Для таких систем V= 3...10 л/мин.
T0=Tвх+(Pa+Pf)/(2cgV) . (84)
На этом и последующих этапах при расчете критериев подобия и условий нагрева воды теплофизические характеристики выбирают по средней температуре водяного потока T0 (табл. 12).
Теплофизические характеристики воды
|
T, 0C |
λ, Вт/(м·град) |
ν·106, м2/с |
γ, кг/м3 |
c, Дж/(кг·град) |
Pr |
|
20 |
0,600 |
1,006 |
998,2 |
4180 |
7,02 |
|
30 |
0,617 |
0,805 |
995,6 |
4180 |
5,42 |
Скорость движения воды v=V/Fк. Соответствующее значение критерия Рейнольдса Re=vdэф/n. По этим данным рассчитывается критерий Нуссельта.
Для системы в виде рубашки охлаждения
Nu=0,015kelRe0,8Pr0,43(Dб/Dан)0,25, (85)
где Dб=Dан+2dа – диаметр бачка. (Расчет поправочных коэффициентов k и el описан в разделе 8.2.1)
Для змеевика и спирального канала справедлива формула (70)
По результатам расчета критерия Нуссельта определяются коэффициент теплоотдачи a=Nul/dэф, а затем – температура анода
Ta=T0+(Pa+Pf)/(aFa0). (86)
Расчет можно считать успешно законченным, если Tа<100 0C.
ПРОГРАММА RELA
Инструкция пользователя при работе в компьютерном классе ФЭ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.