Расчет и проектирование электронных приборов: Учебное пособие, страница 13

В случае цилиндрического анода с внутренними ребрами вместо e_авн и F_авн следует соответственно указывать приведенный коэффициент излучения e’_авн внутренней стороны анода и площадь, «натянутую» на внутреннюю сторону F’_авн, .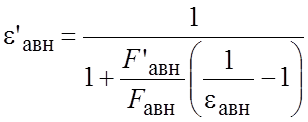

Для такого анода

F_aн = 2π(r_a + t_рвн)h + 2n_рt_рh;   F’_aн ≈ 2π(r_a + t_рвн + t_р)h;

F_aвн = 2π(r_a + t_рвн)h+ 2n_рвнt_рвнh;   F’_aвн ≈ 2πr_ah.

Длину ребер на внутренней стороне анода t_рвн выбирают в пределах 0,5…1 см, а их количество выбирается таким, чтобы расстояние между ребрами примерно совпадало с длиной внутренних ребер.

Значения коэффициента теплового излучения анодных материалов ламп большой и средней мощности приведены в табл. 7.

В случае катода из чистого вольфрама либо катода из карбидированного торированного вольфрама предельно допустимой температурой анода T_доп является температура заметного испарения выбранного материала (табл. 8).

Таблица 7

Коэффициент излучения анодных материалов

Материал	Молибден	Молибден цирконированный	Тантал	Тантал матированный	Ниобий	Графит шероховатый	Графит гладкий
Коэффициент излучения ε	0,08 – 0,192 (900 – 1800 К)	0,7 – 0,8	0,132 – 0,186 (1000 – 1600 К)	0,43 – 0,51  (800 – 1150 К)	0,116 – 0,178 (1000 – 1600 К)	0,89	0,81

Таблица 8

Предельно допустимая температура анода ламп с прямонакальным катодом

Материал	Tдоп, К	Материал	Tдоп, К
Молибден цирконированный	1600	Сплав тантал - ниобий	1500
Тантал	1500	Графит	1800

В случае оксидного катода предельной считается температура, при которой начинается заметное воздействие излучения анода на тепловой режим катода. Этому явлению соответствует температура 500 ⁰ С.

8.2. Тепловой расчет анода с принудительным охлаждением

8.2.1. Общие закономерности

Под принудительной системой охлаждения подразумевают систему конвективного теплоотвода с жидкостным либо воздушным теплоносителем. При соприкосновении молекул жидкости либо газа с поверхностью нагретого тела они приобретают энергию хаотического движения, соответствующую температуре тела. Молекулы, перемещаясь затем вглубь потока, передают полученную энергию общей массе теплоносителя, увеличивая его теплоемкость. В случае воздушной системы охлаждения поток нагретого воздуха рассеивается в окружающее пространство. В случае жидкостной системы приобретенное тепло либо уходит с общим потоком в канализационную сеть, либо передается воздуху через специальные теплообменники. (При проектировании систем охлаждения электронных приборов заключительный этап теплообмена обычно не рассматривается.)

В движущемся потоке можно выделить слой, непосредственно примыкающий к поверхности охлаждаемого тела, где молекулы теплоносителя имеют нулевую скорость. Это дает основание теплопередачу в пограничном слое описывать с помощью уравнения Фурье:

Q = –lF_а dT/dx,                                                (66)

где Q – передаваемый тепловой поток; l –  коэффициент теплопроводности теплоносителя; F_а – площадь охлаждаемой поверхности; dT/dx – градиент температуры по нормали к охлаждаемой поверхности.

Связь отводимого потока с перепадом между температурой стенки T₀ и средней температурой теплоносителя T_s  описывается уравнением Ньютона-Рихмана:

Q = aF_a (T_a –T_s),                                             (67)

где  – коэффициент теплоотдачи.

Условия распространения тепла движущимся потоком описываются уравнением энергии:

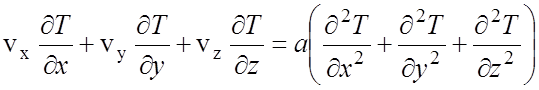 ,                   (68)

где a = λ/(cγ) – коэффициент температуропроводности; c – удельная теплоемкость и γ – плотность теплоносителя (газа либо жидкости); v_x, v_y и v_z – локальные значения скорости потока по координатам  x, y и z соответственно.

Движение теплоносителя описывается тензорным уравнением аэро- гидродинамики – уравнением Навье-Стокса. В наиболее простом виде без учета сил гравитации и изменения давления вдоль движущегося потока уравнение Навье-Стокса по одной из координат тензора (v_x) записывается следующим образом:

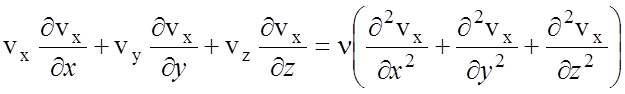 ,               (69)

где ν = μ/γ – коэффициент кинематической вязкости; μ – коэффициент динамической вязкости теплоносителя.

Совместное решение представленной системы уравнений выполнимо лишь для простейшего (одномерного, ламинарного) потока несжимаемой жидкости. В большинстве же случаев расчетные соотношения составляются на основе обработки экспериментальных данных, полученных на макетах. Данные экспериментальных исследований обобщаются методами теории подобия в виде аналитических зависимостей (критериальных уравнений) между безразмерными параметрами (критериями подобия). Выражения для критериев составляются на основе анализа уравнений, описывающих данный процесс. Наименования критериев подобия традиционно обозначаются начальными буквами фамилий известных ученых.

В случае конвективного теплообмена основными критериями подобия являются:

критерий Нуссельта (Nußelt):  ;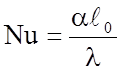

критерий Рейнольдса (Reynolds):   ;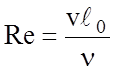

критерий Прандтля (Prandtl):   .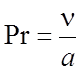

В этих выражениях v – скорость направленного движения теплоносителя, ℓ₀ – определяющий размер системы охлаждения. В случае однородного канала под определяющим размером понимают так называемый «эффективный диаметр» d_эфф= 4S/Π, где S – площадь поперечного сечения, Π – периметр стенок канала охлаждения.

По результатам экспериментальных исследований установлено, что приемлемую точность расчета теплового режима однородного канала обеспечивает следующее критериальное уравнение:

Nu = 0,022ke_lRe^0,8Pr^0,43.                                      (70)

Поправочный коэффициент k в этой формуле зависит от степени турбулентности потока. При Re>10000 режим движения чисто турбулентный. В этом случае k = 1.

Область 2200 < Re<10000 соответствует переходному режиму движения. В этом случае k < 1(табл. 9).

Таблица 9

Значения поправочного коэффициента k в переходном режиме движения

Re	10000	6000	5000	4000	3000	2500	2200
k	1	0,89	0,81	0,65	0,55	0,4	0,27