РЭС и общая характеристика их проектирования. Генерирование корреляционных случайных процессов методом фильтрации. Особенности компьютерного проектирования. Модели объектов проектирования, страница 7

Ограничимся 2 первыми членами. Обозначим t₀=t_k-1, t=t_k, t-t₀=∆t – интервал дискретизации.

 – выражение для расчета прямым методом Эйлера

Рассмотрим обратный метод Эйлера t₀=t_k, t=t_k-1

 – обратный метод Эйлера

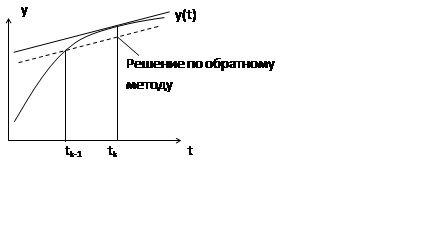Недостатком вычисления по обратному методу Эйлера является неявная зависимость y_k от x_k и y_k-1.

Можно уменьшить ошибку вычисления, если усреднить решение по прямому и обратному методам Эйлера.

 – метод трапеций.

Метод Рунге-Кутта 2-ого порядка:

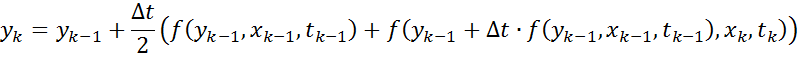
Более высокую точность имеет метод Рунге-Кутта порядка выше второго.

Метод Рунге-Кутта 4-ого порядка:

Метод Рунге-Кутта 4-ого порядка – уточнение угла наклона экстраполирующей прямой – производится по расчету в промежуточной точке в середине интервала ∆t.

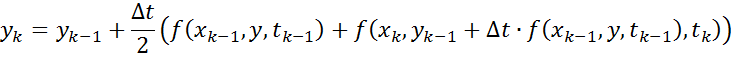
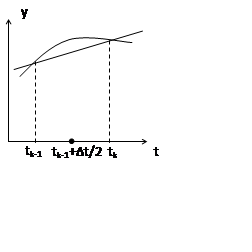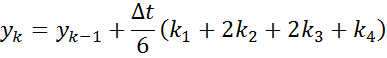
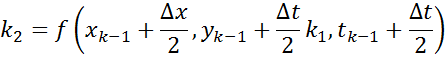
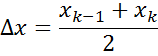
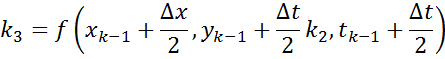
2 вопрос

18 билет

1 вопрос

Расчет выходного процесса линейной системы с использованием интеграла свертки

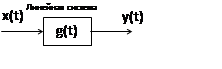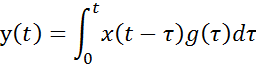
Перейдем к дискретному времени: t=n∆t

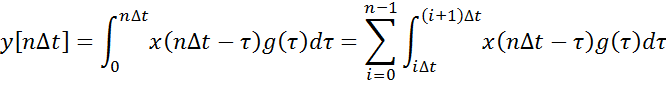
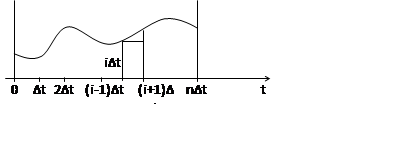
Используем ступенчатую аппроксимацию входного процесса:

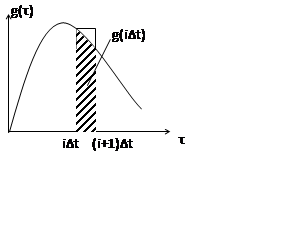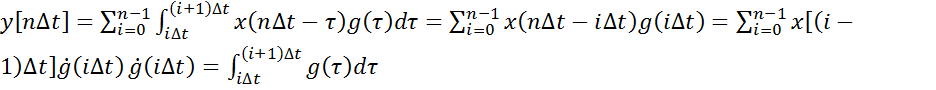
Таким образом, весовые коэффициенты  представляют собой по смыслу площадь под импульсной характеристикой за интервал дискретизации ∆t.

Если ∆t мал, то можно использовать ступенчатую экстраполяцию импульсной характеристики g(τ).

Когда интервал дискретизации мал, то для уменьшения машинного времени можно перейти от большого количества слагаемых к рекуррентной формуле, которая позволяет найти выходной процесс через предыдущие значения выходного процесса.

2 вопрос

Формирование случайных чисел с законом распределения, отличным от равномерного

Можно сформировать случайные числа, используя нелинейные операции.

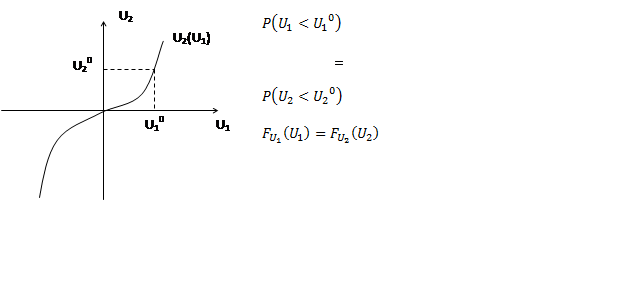Есть 2 числа U₁ и U₂, связанные функциональной зависимостью U₂(U₁) :

19 билет

1 вопрос

Переход от непрерывной передаточной функции к дискретной

Воспользуемся дискретизацией импульсной характеристики

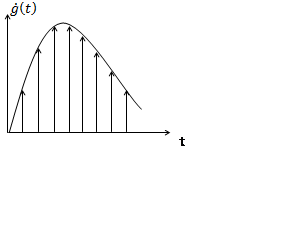
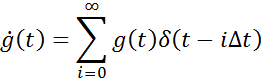
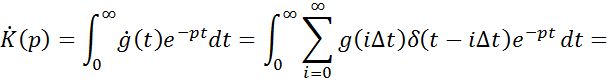
 – дискретное преобразование Лапласа (ДПЛ).

Если e^-p∆t = z → z-преобразование

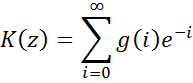
K(p)	K(z)
Интегрирующее звено
Инерционное звено

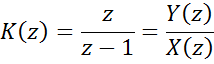
Разностное уравнение

(z-1)Y(z)=zX(z)

y[n+1]-y[n]=x[n+1]

y[n+1]=y[n]+x[n+1]

Возможен переход к дискретной передаточной функции с использованием формул численного интегрирования и заменой в передаточной функции операций аналогового интегрирования дискретным.

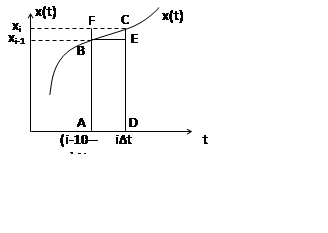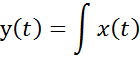
y_i=y_i-1+S_ABCD

Приближенные методы

а)  Метод прямоугольников 1

y_i=y_i-1+∆t∙x_i-1

z-преобразование

Y(z)=z^-1Y(z) +∆t∙z^-1X(z)

Y(z)(1-z^-1)= ∆t∙z^-1X(z)

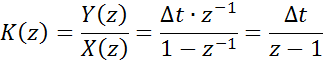
б)  Метод прямоугольников 2

y_i=y_i-1+∆t∙x_i

Y(z)=z^-1Y(z) +∆t∙X(z)

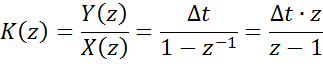
в)  Метод трапеций

y_i=y_i-1+S_{трап ABCD} = y_i-1+∆t(x_i-1+x_i)/2

Z:

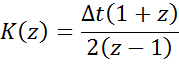
K(p)	K(z)
	Прямоуг 1	Прямоуг 2	Трапеций

Операция по последовательному соединению интеграторов не соответствует операции последовательного соединения дискретных интеграторов.

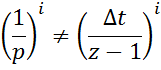
Переход от непрерывной передаточной функции к дискретной совершается следующим образом: числитель и знаменатель непрерывной передаточной функции делится на p в высшей степени полинома знаменателя. В полученном выражении 1/p в соответствии степени знаменателя операцией дискретного интегрирования.

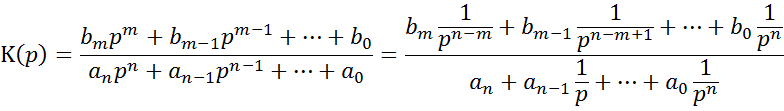
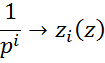
Например: моделирование интегрирующей цепи:

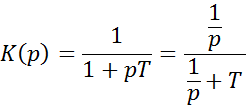
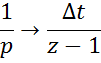
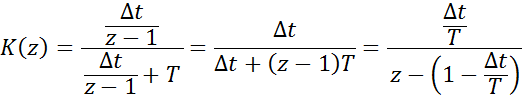
2 вопрос

Генерирование последовательностей со случайной зависимостью

(x₁, x₂, … x_n) – n-мерная случайная величина

n-мерная плотность распределения:

W(x₁, x₂, …x_n)= W(x₁)W(x₂/x₁)W(x₃/x₂,x₁)…W(x_n/x₁,x₂,…x_n-1)

Генерирование случайной последовательности – сложно, используют другие более простые алгоритмы.

1.  Основан на простой цепи Маркова (цепь 1-ого порядка).

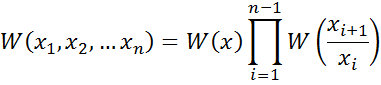
2.  Основан на спектрально-корреляционной теории.

При этой теории вместо n-мерной плотности распределения используется двумерная

W(x_k, x_l)

K и l – любые числа от 1 до n.

Используется второй смешанный момент двумерной плотности распределения.

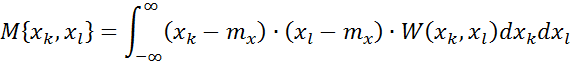
Корреляционный момент.

При использовании данного метода, зависимые случайные величины получаются в результате прохождения независимых случайных величин через линейные цепи

билет 20

1 вопрос

Расчет выходного процесса линейной системы с использованием интеграла свертки

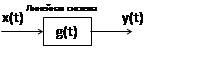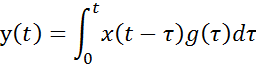
Перейдем к дискретному времени: t=n∆t

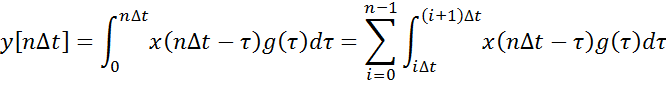
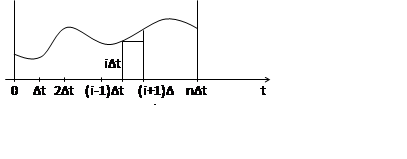
Используем ступенчатую аппроксимацию входного процесса:

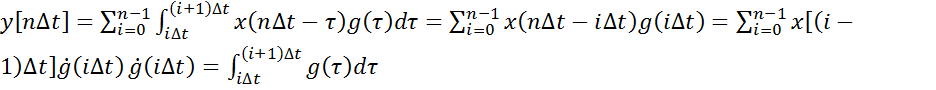
Таким образом, весовые коэффициенты  представляют собой по смыслу площадь под импульсной характеристикой за интервал дискретизации ∆t.

Если ∆t мал, то можно использовать ступенчатую экстраполяцию импульсной характеристики g(τ).

Когда интервал дискретизации мал, то для уменьшения машинного времени можно перейти от большого количества слагаемых к рекуррентной формуле, которая позволяет найти выходной процесс через предыдущие значения выходного процесса.

21 билет

1 вопрос

Планирование эксперимента

Планирование эксперимента предполагает такую организацию исследований, которая обеспечит максимум информации при минимальных затратах. Модель, разработанная при проектировании РЭС, предполагает выбор наилучшего построения РЭС и оптимальный выбор ее параметров.

В теории планирования эксперимента принята следующая терминология.

 

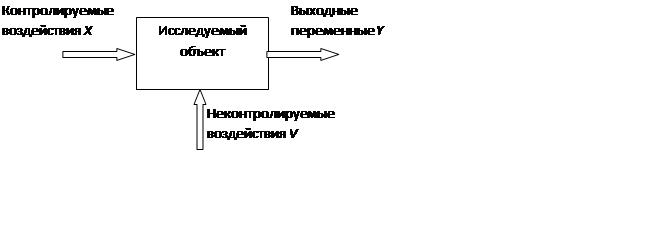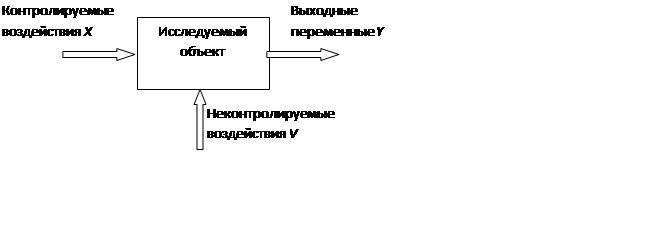
Входные воздействия называются факторами. Значения, которые может принимать входное воздействие, – уровнями фактора.

X = (x₁, x₂,…, x_m),

x_i = (α₁, α₂,…α_l).

x_i – фактор, α_i – уровень фактора.

Выходная переменная Y = (y₁, y₂,…y_n) называется откликом. Зависимость Y(X) называется поверхностью отклика.

Полную информацию об отклике можно получить только при полном переборе факторов, то есть при полном факторном анализе. При большом числе факторов полный факторный анализ связан с большими временными затратами.

Время эксперимента можно сократить, используя следующие приемы:

1) учет априорных сведений, 

2) постепенное усложнение математического описания отклика

3) рандомизация измерений.

и др.

При обработке результатов эксперимента могут возникнуть две ситуации. Первая – когда требуется выяснить функциональную связь между откликом и факторами. И вторая – определить значение факторов, обеспечивающих оптимум отклика.