РЭС и общая характеристика их проектирования. Генерирование корреляционных случайных процессов методом фильтрации. Особенности компьютерного проектирования. Модели объектов проектирования, страница 3

1 схема: непрерывно – детерминированная

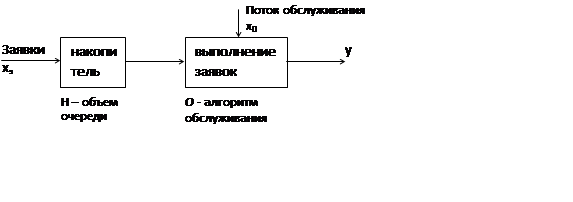
Эта схема используется для описания динамических систем (в которых выходные процессы запаздывают).

d–схема (dynamic system)

математическое описание:

·  Дифференциальное уравнение

·  Интегрированное уравнение

2 схема: дискретно-детерминированная

Используется для математического описания дискретных и цифровых устройств, которые относятся к классу конечных автоматов.

Конечный автомат характеризуется конечным набором входных и выходных значений (конечным алфавитом).

Сам автомат представляет собой цифровую схему:

· 

Без памяти – комбинационные схемы

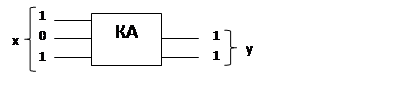·  С памятью – комбинационная схема + триггеры

Для определения связи выходных и входных величин требуется знать внутреннее состояние системы – Z.

Эти переменные связаны между собой функцией перехода и функцией выхода.

Z_k+1=ϕ(Z_k,X_k) – функция перехода

Z_k=ψ(Z_k,X_k) – функция выхода

Математическим описанием является система логических уравнений.

Схема называется f-схема (finite automat)

F=<x, y, z₀, z, ϕ(z,x), ψ(z,x)>

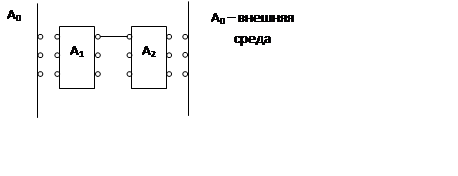
3 схема: дискретно-стохастическая

Используется для вероятностных автоматов (probability automat).

p-схема.

В отличии от конечного автомата, определяющего входной сигнал и состояние системы может соответствовать несколько выходных сигналов, каждый со своей вероятностью появления.

Поэтому вместо функции входа и выхода используется матрица вероятности перехода, из состояния z_k, x_kв состояние z_k+1, y_k.

В-матрица вероятностей перехода-выхода.

P=<x, y, z₀, z, B>

4 схема: g-схема.

Для описания систем массового обслуживания.

Для математического описания сложных систем, к которым не подходит не одна из этих схем, используется А-схема (агрегативная схема).

2 вопрос

Оценка близости законов распределения генерируемой СВ к требуемому закону распределения

Наиболее известными критериями являются:

1.  χ² - Пирсона

2.  Колмогорова

Оценка близости по критерию χ ² - Пирсона производится по величине взвешенной функции квадратичного отклонения плотности распределения СВ и ее оценки.                              

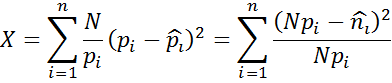
– теоретическое количество попаданий СВ в заданный интервал.

Пирсон доказал, что сумма из n случайных независимых величин, распределяется одинаково, имеет функцию распределения типа χ², которая зависит от числа степеней свободы k=n-s, где n–количество суммируемых величин (здесь – количество разрядов), s–количество независимых условий, накидываемых на n_i.

Например:
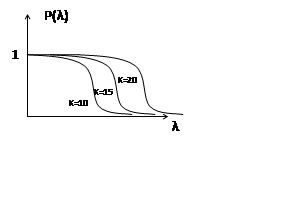
Далее определяется вероятность того, что мера отличия λ будет не меньше значения, определяемого случайным характером измерений.

По этой характеристике, для рассчитанного λ, находят значение P(λ). Если P(λ) достаточно большое (P(λ)>0,1), считают, что гипотеза о близости закона распределения может быть принята.

Билет 7

вопрос 1

Математическая модель по d-схеме

  I.  Непрерывные системы осуществляют как линейную так и нелинейную обработку, если обработки нельзя разделить, то единственное математическим описанием является нелинейное ДУ.

  II.  Если же можно разделить нелинейную и линейную обработку, то модель становится более простой, состоящей из нелинейных блоков, описываемых y=f(x)

и линейных блоков, которые описываются линейным ДУ или связанным с ними другого вида математического описания

Векторно-матричная форма записи

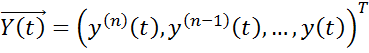
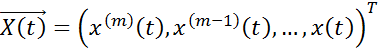
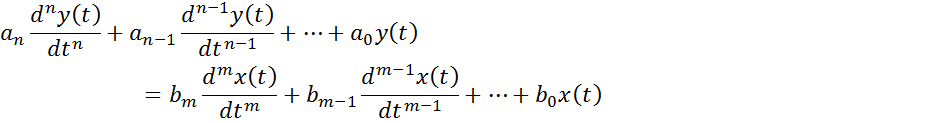
Передаточная функция:

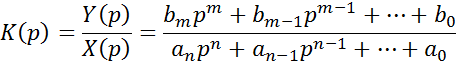
Комплексная частотная характеристика:

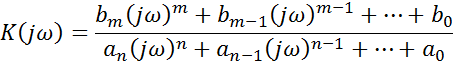
Временные характеристики:

·  импульсная

·  переходная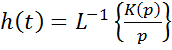

При моделировании линейных систем можно использовать как частотный метод вычисления, так и временной.

Частотный метод:

 – метод установившихся процессов

Временной метод:

              y – для расчета переходных процессов

              y – установившейся процесс

2 вопрос

Генерирование последовательностей со случайной зависимостью

(x₁, x₂, … x_n) – n-мерная случайная величина

n-мерная плотность распределения:

W(x₁, x₂, …x_n)= W(x₁)W(x₂/x₁)W(x₃/x₂,x₁)…W(x_n/x₁,x₂,…x_n-1)

Генерирование случайной последовательности – сложно, используют другие более простые алгоритмы.   Основан на простой цепи Маркова (цепь 1-ого порядка).

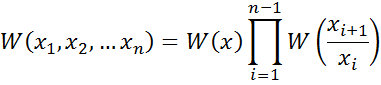
1.  Основан на спектрально-корреляционной теории.

При этой теории вместо n-мерной плотности распределения используется двумерная

W(x_k, x_l)

K и l – любые числа от 1 до n.

Используется второй смешанный момент двумерной плотности распределения.

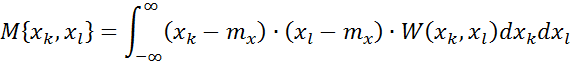
Корреляционный момент.               

При использовании данного метода, зависимые случайные величины получаются в результате прохождения независимых случайных величин через линейные цепи.

Билет 8

1 вопрос

Численное решение нелинейных ДУ

Рассмотрим на основе НДУ 1-ого порядка

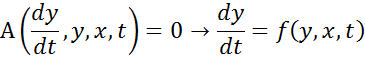
Численное решение позволяет в какой-либо момент времени найти выходное значение по значению входного процесса в этот момент и выходной в предыдущий момент.

Численное решение основано на использовании разложения в ряд Тейлора.

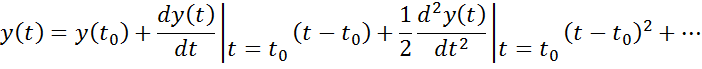
Ограничимся 2 первыми членами. Обозначим t₀=t_k-1, t=t_k, t-t₀=∆t – интервал дискретизации.

 – выражение для расчета прямым методом Эйлера

Рассмотрим обратный метод Эйлера t₀=t_k, t=t_k-1

 – обратный метод Эйлера

Недостатком вычисления по обратному методу Эйлера является неявная зависимость y_k от x_k и y_k-1.

Можно уменьшить ошибку вычисления, если усреднить решение по прямому и обратному методам Эйлера.

 – метод трапеций.

Метод Рунге-Кутта 2-ого порядка:

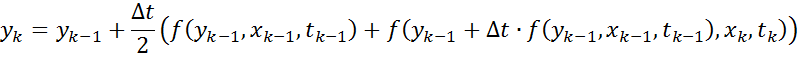
Более высокую точность имеет метод Рунге-Кутта порядка выше второго.

Метод Рунге-Кутта 4-ого порядка:

Метод Рунге-Кутта 4-ого порядка – уточнение угла наклона экстраполирующей прямой – производится по расчету в промежуточной точке в середине интервала ∆t.

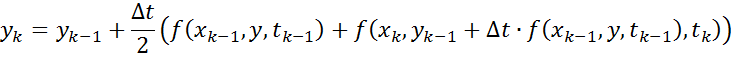
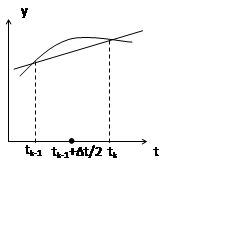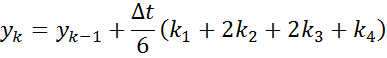
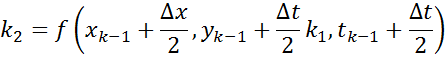
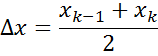
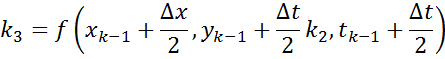
2 вопрос

Наиболее известными критериями являются:

1.  χ² - Пирсона

2.  Колмогорова

Оценка близости по критерию χ ² - Пирсона производится по величине взвешенной функции квадратичного отклонения плотности распределения СВ и ее оценки.

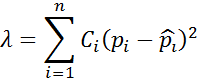
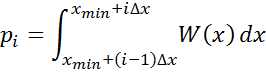
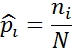
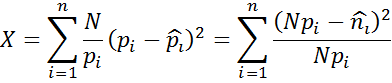
– теоретическое количество попаданий СВ в заданный интервал.