РЭС и общая характеристика их проектирования. Генерирование корреляционных случайных процессов методом фильтрации. Особенности компьютерного проектирования. Модели объектов проектирования, страница 4

Пирсон доказал, что сумма из n случайных независимых величин, распределяется одинаково, имеет функцию распределения типа χ², которая зависит от числа степеней свободы k=n-s, где n–количество суммируемых величин (здесь – количество разрядов), s–количество независимых условий, накидываемых на n_i.

Например:

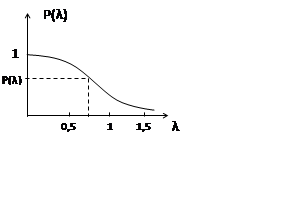
Далее определяется вероятность того, что мера отличия λ будет не меньше значения, определяемого случайным характером измерений.

По этой характеристике, для рассчитанного λ, находят значение P(λ). Если P(λ) достаточно большое (P(λ)>0,1), считают, что гипотеза о близости закона распределения может быть принята.

Критерий Колмогорова

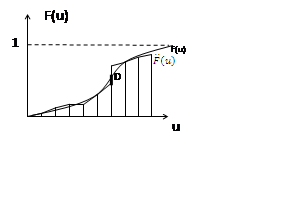
Критерий требует сравнения не плотностей вероятности, а функции распределения.

D – максимальное отличие.

Колмогоров показал, что максимальное отличие (D) функции распределения и ее оценки имеет закон распределения не зависящий от закона распределения случайной величины u, и поэтому можно оценить близость закона распределения по максимальному D.

Если P(λ)>0,1, то гипотеза о близости законов распределения может быть принята.

Эти критерии по-разному учитывают значимость распределений в центре и по краям. Если необходимо учитывать с большим весом отличия на краях используют χ² – Пирсона. Различие в центре распределения – критерий Колмогорова.

Билет 9

1 вопрос

Расчет выходного процесса линейной системы с использованием интеграла свертки

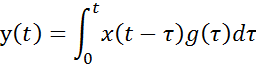
Перейдем к дискретному времени: t=n∆t

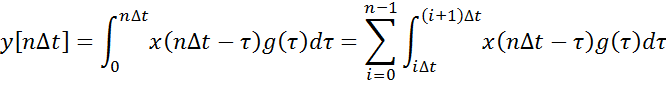
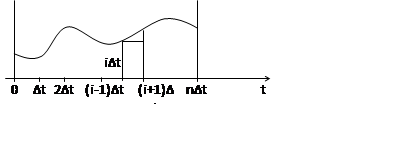
Используем ступенчатую аппроксимацию входного процесса:

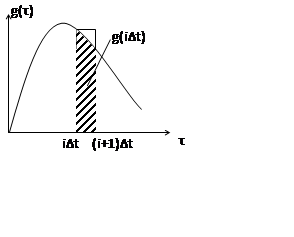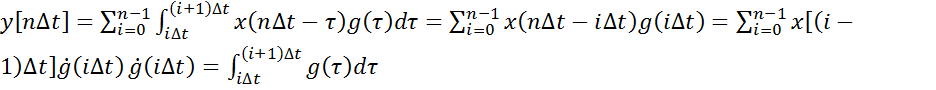
Таким образом, весовые коэффициенты  представляют собой по смыслу площадь под импульсной характеристикой за интервал дискретизации ∆t.

Если ∆t мал, то можно использовать ступенчатую экстраполяцию импульсной характеристики g(τ).

Когда интервал дискретизации мал, то для уменьшения машинного времени можно перейти от большого количества слагаемых к рекуррентной формуле, которая позволяет найти выходной процесс через предыдущие значения выходного процесса.

2 вопрос

Моделирование воздействий

Для моделирования детерминированных воздействий используется задание формулой:

Например:     

Операции производятся как суммирование конечного числа членов ряда. Можно использовать рекуррентное соотношение:

Недостаток – накопление ошибок округления.

              Для формирования случайных воздействий используется 3 способа:

1.  Аппаратный (физический)

2.  Программный (алгоритмический)

3.  Числовой (файловый)

Показатели	Аппаратный	Алгоритмический	Числовой
Длина реализации	Не ограничен	Ограничен псевдослуч. процессом	Ограничен объемом памяти
Повторяемость реализации	Повторяемости нет	Повторяемость полная	Повторяемость полная
Стабильность характеристик	Низкая	Высокая	Высокая
Минимальный интервал дискретизации	Быстродействие АЦП	Время вычисления Xi	Время обращения к памяти

10 билет

1 вопрос

Переход от непрерывной передаточной функции к дискретной

Воспользуемся дискретизацией импульсной характеристики

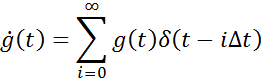
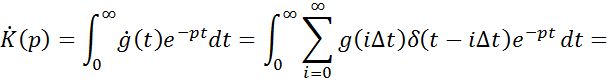
 – дискретное преобразование Лапласа (ДПЛ).

Если e^-p∆t = z → z-преобразование

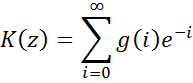
K(p)	K(z)
Интегрирующее звено
Инерционное звено

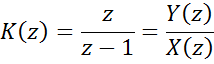
Разностное уравнение

(z-1)Y(z)=zX(z)

y[n+1]-y[n]=x[n+1]

y[n+1]=y[n]+x[n+1]

Возможен переход к дискретной передаточной функции с использованием формул численного интегрирования и заменой в передаточной функции операций аналогового интегрирования дискретным.

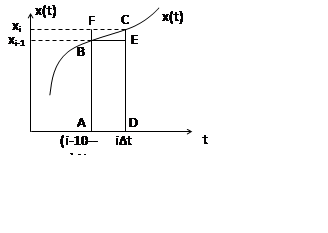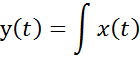
y_i=y_i-1+S_ABCD

Приближенные методы

а)  Метод прямоугольников 1

y_i=y_i-1+∆t∙x_i-1

z-преобразование

Y(z)=z^-1Y(z) +∆t∙z^-1X(z)

Y(z)(1-z^-1)= ∆t∙z^-1X(z)

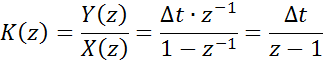
б)  Метод прямоугольников 2

y_i=y_i-1+∆t∙x_i

Y(z)=z^-1Y(z) +∆t∙X(z)

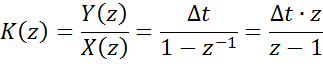
в)  Метод трапеций

y_i=y_i-1+S_{трап ABCD} = y_i-1+∆t(x_i-1+x_i)/2

Z:

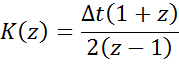
K(p)	K(z)
	Прямоуг 1	Прямоуг 2	Трапеций

Операция по последовательному соединению интеграторов не соответствует операции последовательного соединения дискретных интеграторов.

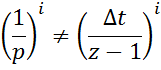
Переход от непрерывной передаточной функции к дискретной совершается следующим образом: числитель и знаменатель непрерывной передаточной функции делится на p в высшей степени полинома знаменателя. В полученном выражении 1/p в соответствии степени знаменателя операцией дискретного интегрирования.

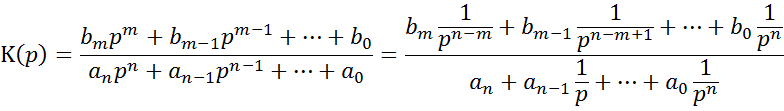
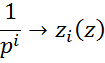
Например: моделирование интегрирующей цепи:

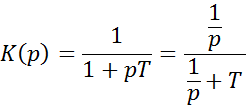
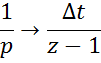
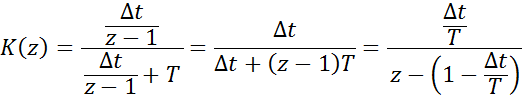
2 вопрос

Формирование случайных чисел с законом распределения, отличным от равномерного

Можно сформировать случайные числа, используя нелинейные операции.

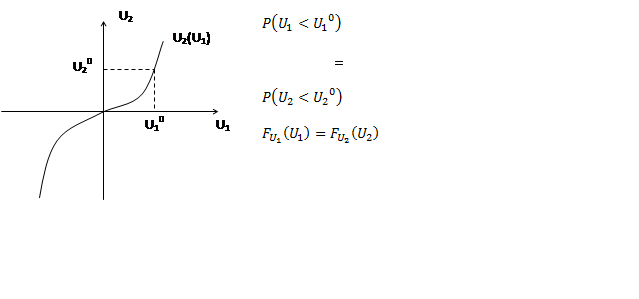Есть 2 числа U₁ и U₂, связанные функциональной зависимостью U₂(U₁) :

На этом соотношении основан метод обратной функции. Требуется сформировать случайную величину U с плотностью вероятности w_u(u) из случайной величины X, равномерно распределеннй в интервале (0,1).

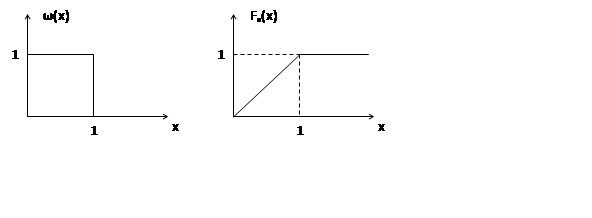
Найти функцию u(x)

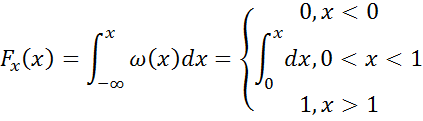
 – обратная функция

Например для экспоненциального распределения

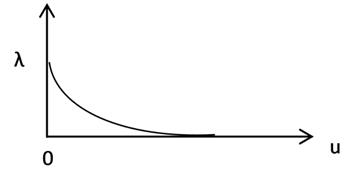
1 – e^-λu=x

e^-λu=1 – x

-λu=ln(1 - x)

u=-1/λ∙ ln(1 - x)

Методом обратной функции можно найти функциональную связь между случайными величинами только для ограниченного числа видов распределения.

Не требует каких-либо аналитических выражений для преобразования случайных величин метод отбора.

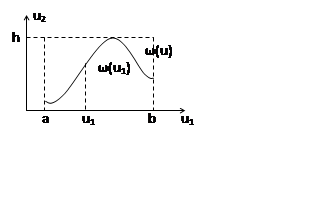Позволяет получить случайную величину, если известен закон распределения.

Отбор производится пропорционально ее плотности вероятности по следующему алгоритму:

1.  Генерируется пара равномернораспределенных случайных чисел

U₁ в интервале (a,b) и случайная величина U₂  в (0,h).

2.  Проверяется, находится ли точка с координатами (U₁, U₂) ниже плотности распределения ω(u).

Решение: если (U₁, U₂) ниже ω(u), то принимается решение u= u₁, т.е. считается что значение u₁ ϵ u, если (U₁, U₂) выше ω(u), то испытания повторяются, а результат не учитывается.

Алгоритм генерирования: