1. Генерируется случайная величина x1 равномернораспределенная в интервале (0,1).
2. Рассчитывается случайная величина U1 равномернораспределенная в интервале (a,b). u1=a-x(a-b).
3. Определяется значение плотности вероятности ω(u1).
4. Генерируется случайная величина x2 равномернораспределенная в интервале (0,1).
5. Рассчитывается U2=x2∙h, равномернораспределенная в интервале (0,h).
6. Если u2 < ω(u1), то u=u1, если u2 > ω(u1), то значение u1 обрабатывается.
7. Генерируется следующая пара чисел u1 и u2 и т.д.
11 билет
1 вопрос
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
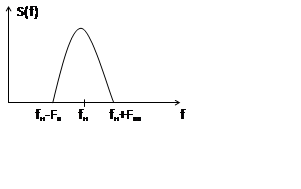 |
При моделировании используются 3 метода:
1. Метод несущей
2. Метод комплексной огибающей
3. Метод информационного параметра
Метод несущей
При использовании этого метода модель фактически повторяет структуру моделирующего устройства, а частота дискретизации выбирается исходя из теоремы Котельникова.
fд ≥ 2(fн+Fв)
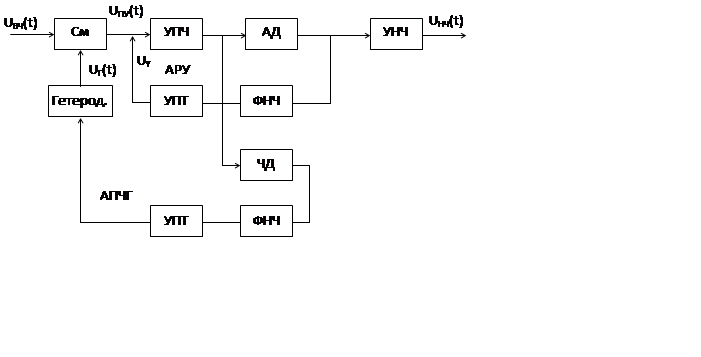
Модель радиоприемного устройства
 |
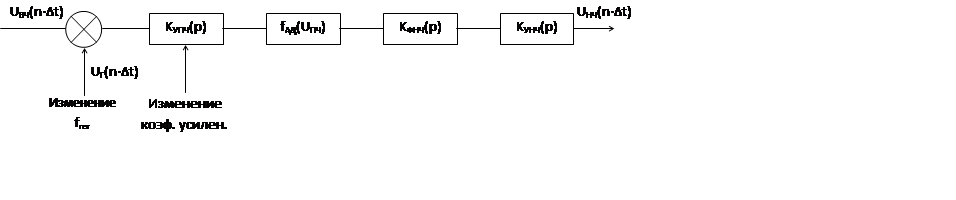 |
Недостаток моделирования – высокая тактовая частота. Для ее уменьшения используют масштабирования.
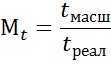
Используется два вида масштабирования:
1. Применяется по всем параметрам сигнала и устройства обработки одинаково.
![]()
Все процессы замедляются в Mt раз по сравнению с реальным временем. Такое масштабирование во много раз увеличивает время моделирования по сравнению с реальным.
2. Масштаб для несущей и огибающей различны
![]()
![]()
Такое масштабирование физически основано на том, что при изменении несущей частоты в каких-то пределах, огибающая не изменяется.
Минимальное значение частоты дискретизации в этом случае определяется обобщенной теоремой Котельникова.
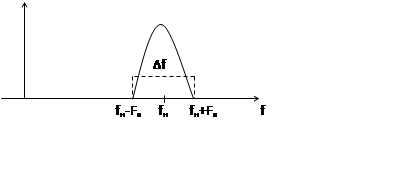 |
fдискр min ≥ 2∆f ≥ 4Fв
Использование такого метода экономит время моделирования.
2 вопрос
12 билет
1 вопрос
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
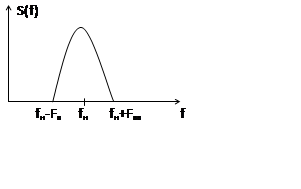 |
При моделировании используются 3 метода:
4. Метод несущей
5. Метод комплексной огибающей
6. Метод информационного параметра
метод комплексной огибающей
Метод несущей характеризуется избыточностью, т.к. сама несущая не несет полезной информации.
В методе комплексной огибающей несущая вообще не учитывается, а моделирование ведется по комплексной огибающей.
ВЧ сигнал: ![]()
Um(t) – амплитудная модуляция
ϕ(t) – угловая модуляция (ЧМ или ФМ)
Устройство обработки является узкополосным, поэтому его импульсная характеристика является колебательной.
![]()
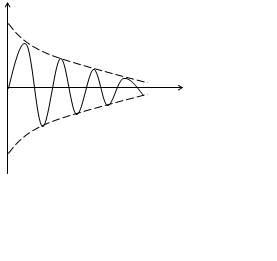 |
![]()
При записи комплексной огибающей учтем, что центральная частота ВЧ колебаний может не совпадать с центральной частотой настройки устройства обработки
![]()
![]()
![]()
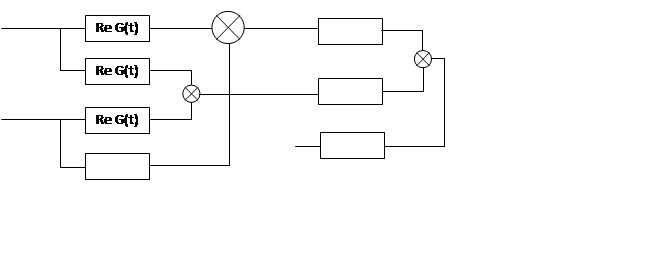
Модель построена по формуле свертки, которая справедлива для комплексной огибающей.
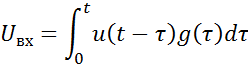
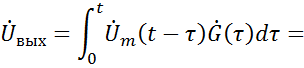
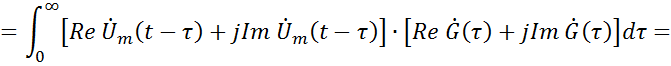
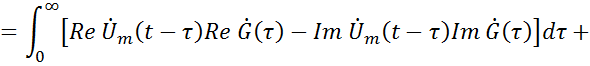
 |
 |
2 вопрос
Формирование случайных чисел с законом распределения, отличным от равномерного
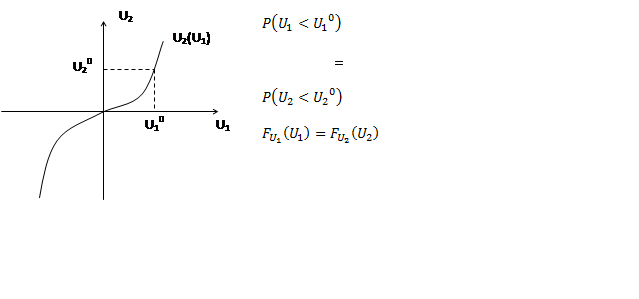 |
Есть 2 числа U1 и U2, связанные функциональной зависимостью U2(U1) :
На этом соотношении основан метод обратной функции. Требуется сформировать случайную величину U с плотностью вероятности wu(u) из случайной величины X, равномерно распределеннй в интервале (0,1).
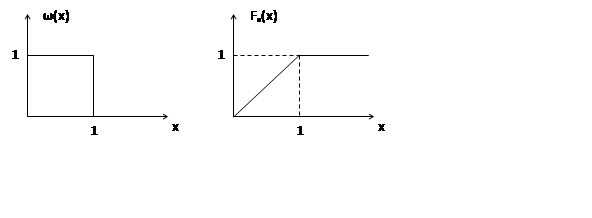
Найти функцию u(x)
![]()
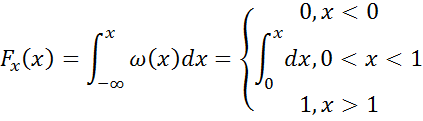
![]() – обратная функция
– обратная функция
Например для экспоненциального распределения
![]()
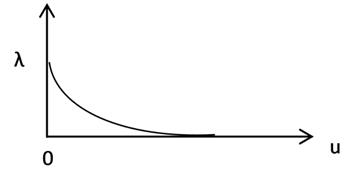
![]()
1 – e-λu=x
e-λu=1 – x
-λu=ln(1 - x)
u=-1/λ∙ ln(1 - x)
Методом обратной функции можно найти функциональную связь между случайными величинами только для ограниченного числа видов распределения.
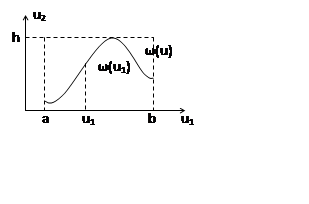
Не требует каких-либо
аналитических выражений для преобразования случайных величин
13 билет
1 вопрос
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
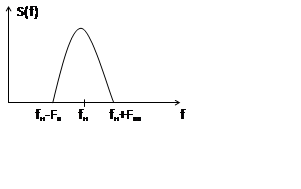 |
При моделировании используются 3 метода:
1. Метод несущей
2. Метод комплексной огибающей
3. Метод информационного параметра
4. Метод информационного параметра
5. Под информационным параметром понимается медленное изменение количества параметра радиосигнала: частоты, амплитуды или фазы.
6. Данный метод используется при моделировании систем АПЧ (систем радиоавтоматики).
7. Например, в приемнике, который мы моделировали, есть две петли автоподстройки: автоматическое регулирование усиления и автоматическая подстройка частоты гетеродина.
8. При моделировании не учитываем ни несущую частоту, ни огибающую.
9. Составим модель для метода информационного параметра для АПЧ:
10.
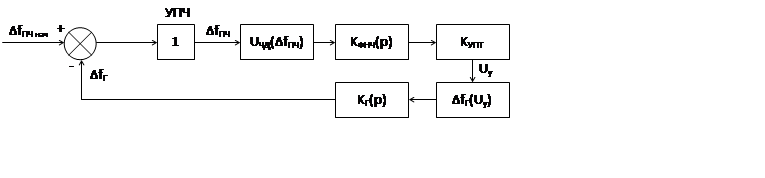
11.
Билет 14
1 вопрос
Численное решение нелинейных ДУ
Рассмотрим на основе НДУ 1-ого порядка
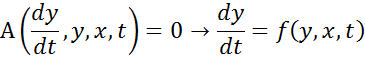
Численное решение позволяет в какой-либо момент времени найти выходное значение по значению входного процесса в этот момент и выходной в предыдущий момент.
 |
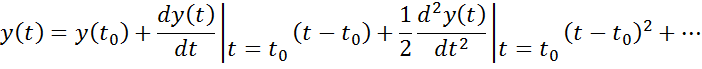
Ограничимся 2 первыми членами. Обозначим t0=tk-1, t=tk, t-t0=∆t – интервал дискретизации.
![]()
![]() – выражение для расчета прямым методом Эйлера
– выражение для расчета прямым методом Эйлера
Рассмотрим обратный метод Эйлера t0=tk, t=tk-1
![]()
![]()
![]()
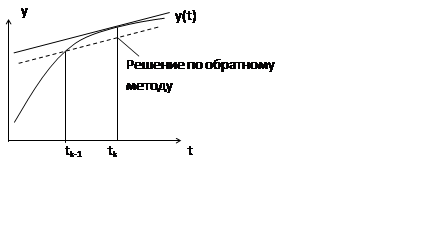 |
Недостатком вычисления по обратному методу Эйлера является неявная зависимость yk от xk и yk-1.
Можно уменьшить ошибку вычисления, если усреднить решение по прямому и обратному методам Эйлера.
![]() – метод трапеций.
– метод трапеций.
Метод Рунге-Кутта 2-ого порядка:
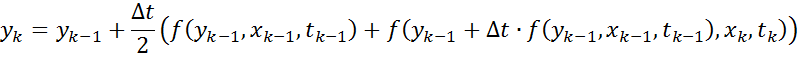
Более высокую точность имеет метод Рунге-Кутта порядка выше второго.
Метод Рунге-Кутта 4-ого порядка:
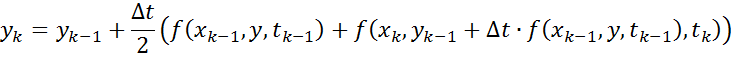
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.