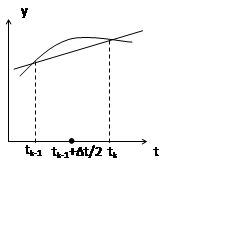 |
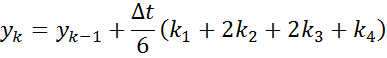
![]()
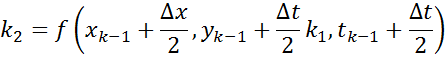
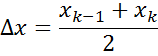
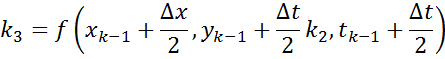
![]()
2 вопрос
15 билет
1 вопрос
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
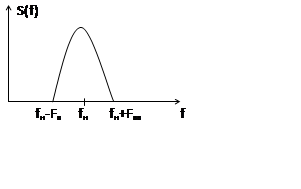 |
При моделировании используются 3 метода:
1. Метод несущей
2. Метод комплексной огибающей
3. Метод информационного параметра
Метод комплексной огибающей
Метод несущей характеризуется избыточностью, т.к. сама несущая не несет полезной информации.
В методе комплексной огибающей несущая вообще не учитывается, а моделирование ведется по комплексной огибающей.
ВЧ сигнал: ![]()
Um(t) – амплитудная модуляция
ϕ(t) – угловая модуляция (ЧМ или ФМ)
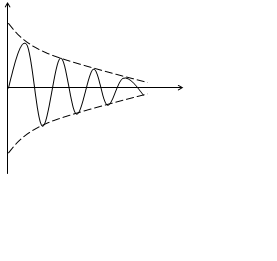
Устройство обработки является узкополосным, поэтому его импульсная характеристика является колебательной.
![]()
 |
![]()
При записи комплексной огибающей учтем, что центральная частота ВЧ колебаний может не совпадать с центральной частотой настройки устройства обработки
![]()
![]()
![]()
Модель построена по формуле свертки, которая справедлива для комплексной огибающей.
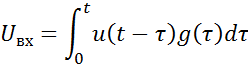
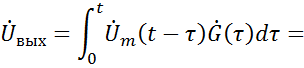
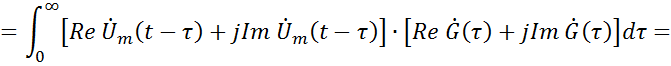
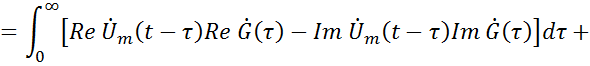
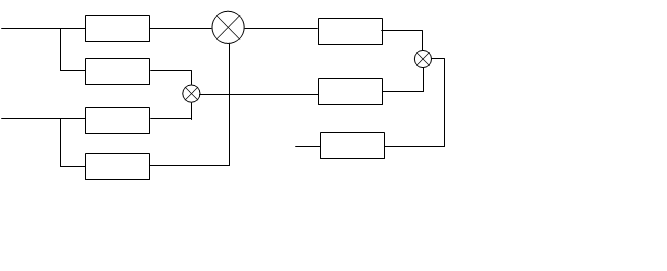 |
 |
2 вопрос
Оценка близости законов распределения генерируемой СВ к требуемому закону распределения
Наиболее известными критериями являются:
1. χ2 - Пирсона
2. Колмогорова
Оценка близости по критерию χ 2 - Пирсона производится по величине взвешенной функции квадратичного отклонения плотности распределения СВ и ее оценки.
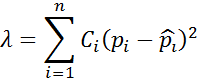
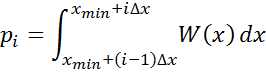
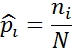
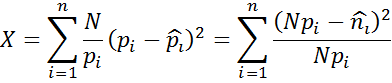
![]() – теоретическое количество попаданий СВ в заданный интервал.
– теоретическое количество попаданий СВ в заданный интервал.
Пирсон доказал, что сумма из n случайных независимых величин, распределяется одинаково, имеет функцию распределения типа χ2, которая зависит от числа степеней свободы k=n-s, где n–количество суммируемых величин (здесь – количество разрядов), s–количество независимых условий, накидываемых на ni.
Например: ![]()
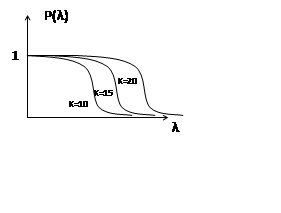
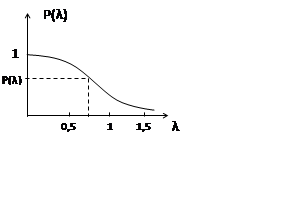
Далее определяется вероятность
того, что мера отличия λ
будет не меньше значения, определяемого случайным характером измерений.
По этой характеристике, для рассчитанного λ, находят значение P(λ). Если P(λ) достаточно большое (P(λ)>0,1), считают, что гипотеза о близости закона распределения может быть принята.
Критерий Колмогорова
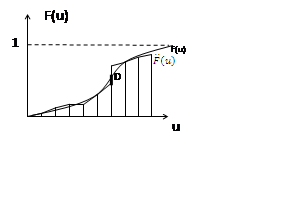
Критерий требует сравнения не плотностей вероятности, а функции распределения.
D – максимальное отличие.
Колмогоров показал, что максимальное отличие (D) функции распределения и ее оценки имеет закон распределения не зависящий от закона распределения случайной величины u, и поэтому можно оценить близость закона распределения по максимальному D.
 |
![]()
Если P(λ)>0,1, то гипотеза о близости законов распределения может быть принята.
Эти критерии по-разному учитывают значимость распределений в центре и по краям. Если необходимо учитывать с большим весом отличия на краях используют χ2 – Пирсона. Различие в центре распределения – критерий Колмогорова.
16 билет
1 вопрос
Моделирование узкополосных радиотехнических устройств
Для моделирования таких устройств характерно, что спектр сосредоточен на fн и в узком диапазоне.
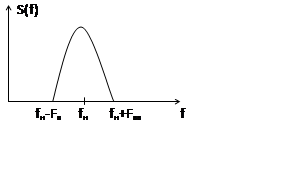 |
При моделировании используются 3 метода:
1. Метод несущей
2. Метод комплексной огибающей
3. Метод информационного параметра
Метод информационного параметра
Под информационным параметром понимается медленное изменение количества параметра радиосигнала: частоты, амплитуды или фазы.
Данный метод используется при моделировании систем АПЧ (систем радиоавтоматики).
Например, в приемнике, который мы моделировали, есть две петли автоподстройки: автоматическое регулирование усиления и автоматическая подстройка частоты гетеродина.
При моделировании не учитываем ни несущую частоту, ни огибающую.
Составим модель для метода информационного параметра для АПЧ:
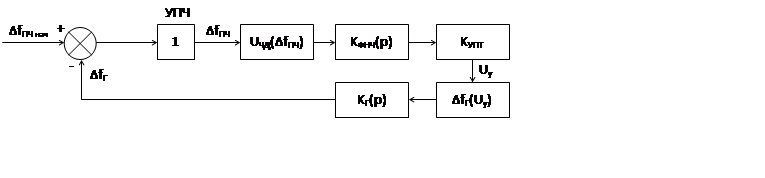
2 вопрос
Восстановление сигнала по его дискретным отсчетам с использованием фиксаторов нулевого и 1-ого порядка
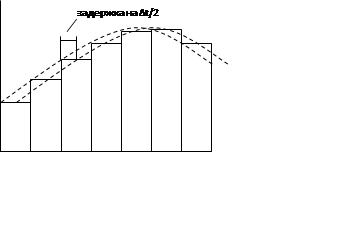 |
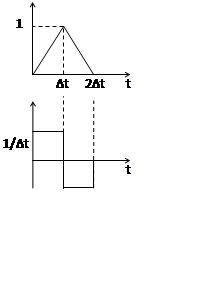
Экстраполяция значения процесса на интервале дискретизации.
 |
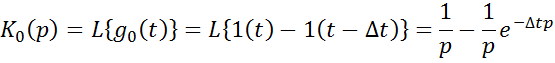
Комплексная частотная характеристика
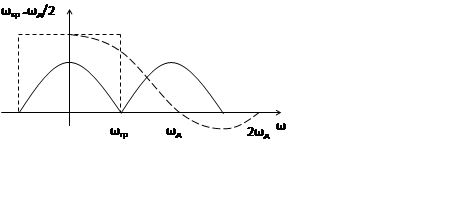 |
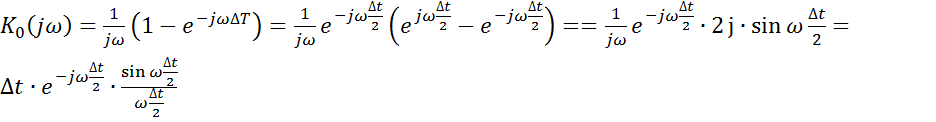 Фиксатор нулевого порядка будет хуже
идеального восстанавливающего фильтра, т.к.:
Фиксатор нулевого порядка будет хуже
идеального восстанавливающего фильтра, т.к.:
1. В пределах ±ωгр коэффициент передачи фиксатора нулевого порядка меньше единицы и изменяется по частоте
2. За пределами полосы пропускания идеального фильтра
|ω|>ωгр коэффициент передачи отличен от нуля.
Тем самым оказывается подчеркнутыми ВЧ составляющие не входящие в спектр частотного сигнала. Нужно повышать ωд, чтобы уменьшить эти ошибки.
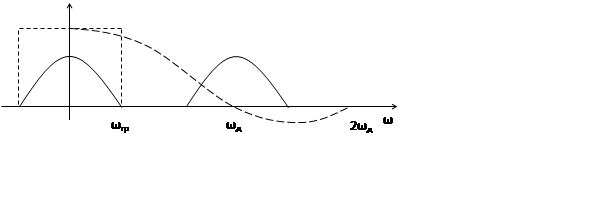 |
Видим, что коэффициент передачи фиксатора в пределах |ω|<ωгр приближается к единице, а в диапазоне ω>ωгр появились свободные от спектра участки, и значит, уменьшились ВЧ искажения.
При моделировании берется ωд 3-5 (2ωгр)
 |
 |
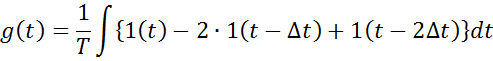
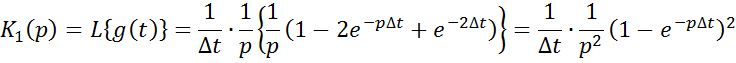
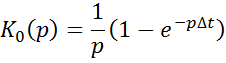
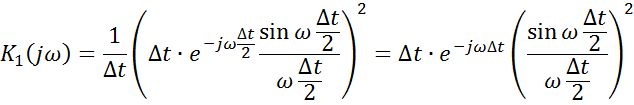
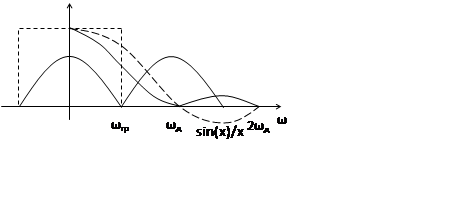 |
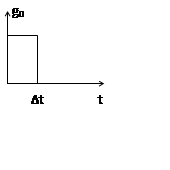
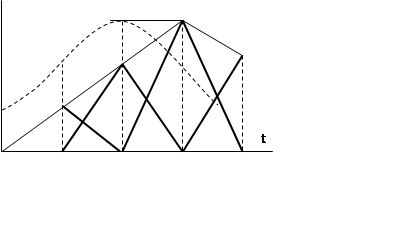
Использование фиксатора 1-ого порядка приводит к значительному падению ВЧ составляющих на |ω|>ωгр. Хотя отличие АЧХ от 1 в области частот |ω|<ωгр стало больше.
Но главный недостаток фиксатора 1-ого порядка является задержка восстановленного сигнала на интервал дискретизации, поэтому при моделировании такой фиксатор используется редко.
17 билет
1 вопрос
Численное решение нелинейных ДУ
Рассмотрим на основе НДУ 1-ого порядка
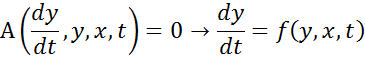
Численное решение позволяет в какой-либо момент времени найти выходное значение по значению входного процесса в этот момент и выходной в предыдущий момент.
 |
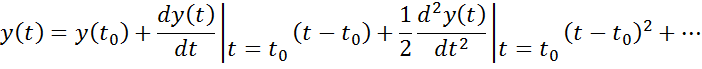
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.