О возможностях и ограничениях p-теоремы. Подобие физических явлений, страница 5

1.  Какие величины надо измерять в опыте;

2.  Как обрабатывать результат;

3.  Каким образом однозначно определить подобные изучаемому явления.

На эти три вопроса ответы дают теоремы подобия.

Понятие и определение подобия физических явлений

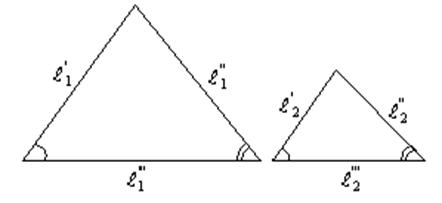
      Впервые с понятием подобия мы встречаемся в геометрии, когда изучаем подобные геометрические фигуры. Известно, что геометрически подобные фигуры обладают тем свойством, что их соответственные углы равны, а сходственные стороны пропорциональны.

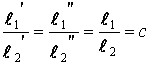                                                   ,                                         (6.1)

где: , ,  – линейные размеры (длины сторон) одной фигуры; , ,  – сходственные линейные размеры другой фигуры.

Коэффициент пропорциональности – «» обычно называют константой подобия.

Очевидно, что условие (6.1) представляет собой математическую формулировку наличия геометрического подобия. Оно должно выполняться для любых сходственных отрезков подобных фигур, например высот, биссектрис, медиан и т.д.

      Также как в случае геометрического подобия можно установить подобие любых физических явлений: кинематическом подобии течения двух потоков газа; тепловом подобии двух процессов теплообмена; динамическом подобии сил, вызывающих подобные между собой движения. При этом необходимо выявить те условия, которые обеспечивают достоверность наличия факта подобия.

      Если речь идет о подобии физических явлений, то оно может иметь место лишь между явлениями одной и той же природы, такие явления качественно одинаковы и описываются одинаковыми уравнениями. Могут иметь место случаи, когда форма математического описания двух физических явлений одна и та же, но они различны по своей физической сущности, то есть разнородны. В этом случае можно вести речь лишь об аналогии между ними, но подобие между такими явлениями отсутствует. В качестве примеров можно привести электрогидродинамическую аналогию и аналогию между диффузией и теплопроводностью.

      Подобные физические явления развиваются в геометрически подобных системах. Это означает, что физическому подобию должно обязательно сопутствовать геометрическое подобие объектов и окружающей среды. Нельзя искать подобие между процессами обтекания цилиндра, сферы, плоской пластины.

      Анализируя подобные физические явления, необходимо сравнивать между собой (сопоставлять) лишь однородные величины в сходственных точках пространства и в сходственные моменты времени. Однородными называются величины, имеющие один  и тот же физический смысл и одинаковую размерность.

      В геометрически подобных пространствах к сходственным точкам относятся те, координаты которых связаны между собой соотношениями подобия

, , ,

где  – константа подобия линейных размеров. Два момента времени  и  считаются сходственными, если они имеют общее начало отсчета и связаны между собой преобразованием подобия .

      Подобие двух физических явлений будет иметь место только тогда, когда подобны все характеризующие их величины