О возможностях и ограничениях p-теоремы. Подобие физических явлений, страница 3

 – однофазная зона,

 – двухфазная зона.

          Выразим каждое из  через основные единицы

;

;

;

;

.

Где , , ,  – показатели степени. Заменим в каждом все величины их размерностями.

;

;

;

;

.

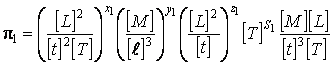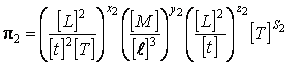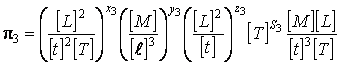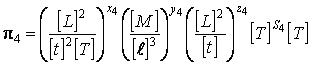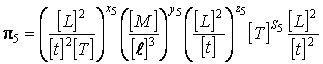Полученные уравнения преобразуем к виду

.

Все пять критериев должны быть безразмерными. Это выполняется в случае, если тождественны будут следующие системы уравнений:

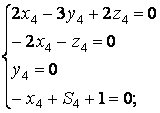
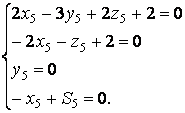
Решая каждую систему в отдельности, получим значения для показателей степени :

Подставляя численные значения в выражения критериев, получим

; ; ;

; .

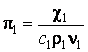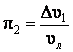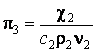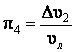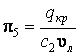Рассмотрим полученные критерии подобия

;  – критерий Прандтля для интервала температуры .

; где .

,  – критерий Прандтля для интервала температуры .

; где .

 – критерий фазового перехода.

Базовая комплексная функциональная зависимость может быть записана в виде

.

Последнее уравнение может быть упрощено путем комбинаций безразмерных комплексов