Теория размерностей и фракционный анализ, страница 5

         При решении практических задач особое значение имеет переход от одних единиц измерения к другим. Рассмотрим необходимое и достаточное условие замены одних единиц измерения другими. Пусть при решении задачи используются уже привычные первичные размерности ,  и . Выберем теперь в качестве первичных некоторые другие – , , . Это можно сделать в том случае, если:

1) размерности , ,  являются независимыми функциями ,  и , то есть

   при любых  и ;

2) возможно однозначное обратное преобразование, то есть , ,  единственным образом можно выразить через , , .

         Пусть величины , ,  имеют размерности

,

,

.

         Прологарифмируем эти выражения

         Такая система уравнений имеет единственное решение в том случае, если определитель, составленный из коэффициентов уравнения, отличен от нуля.

.

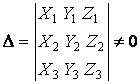Выполнение данного условия указывает на выполнение, как первого, так и второго условий.

2.4. p – теорема

Она устанавливает связь между функцией, выраженной через размерные параметры, и функцией в безразмерной форме. Под безразмерными параметрами мы будем понимать комплексы размерных величин, составленные так, что они не имеют размерности. Это позволяет в дальнейшем сопоставлять и обобщать результаты. Во-вторых, применение безразмерных параметров позволяет уменьшить число независимых координат. В любой физической задаче мы имеем один или несколько зависимых параметров, каждый из которых является функцией некоторых независимых параметров. Обозначим зависимый параметр через . Пусть число независимых параметров равно  Обозначим их . Тогда

,

где  – неизвестная функция. Это уравнение эквивалентно соотношению

,

где  – также неизвестная функция.

Сформулируем суть самой p – теоремы. Если имеется соотношение между  параметрами в виде

,