Теория размерностей и фракционный анализ

Лекции по предмету:

«Теория подобия и размерности»

ЛЕКЦИЯ 1

Физика – наука, использующая в своем развитии как теоретические, так и экспериментальные методы. И в том, и в другом случае она не может обойтись без математики, без того, чтобы не довести результат до числа, до количественной характеристики. Эффективное применение теоретических предпосылок, моделей для практических целей возможно лишь тогда, когда они выражены в количественных соотношениях и позволяют получать численные значения интересующих величин-параметров.

         Наиболее достоверным является путь постановки экспериментального исследования натуральных объектов в натуральных условиях, что практически не всегда возможно. Например, как в натуральных условиях на Земле опытным путем изучать характер процессов, протекающих внутри звезд.

         Большинство попыток найти аналитическое решение физических задач связано с достаточно большими трудностями, обойти которые возможно лишь путем принятия тех или иных упрощающих предпосылок, вносимых в процесс постановки задачи или в ходе ее решения. Поэтому получаемые результаты имеют в лучшем случае характер приближенной оценки, в худшем – они не правильны по своей сути и могут привести к достаточно глубоким заблуждениям.

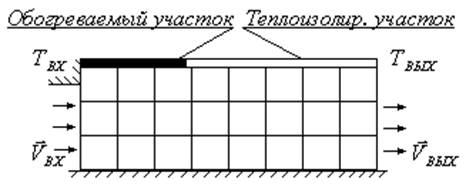
         Существует еще и третий путь исследований. Это численное решение физических задач. Как и при чисто аналитическом, пути исследования при получении численных решений анализируются результаты решения некоторой используемой математической модели, а не характеристики действительного физического процесса. В большинстве инженерных задач в основу положены физические процессы, математические модели которых, главным образом, состоят из систем дифференциальных уравнений. Чисто в аналитическом виде решение можно получить, лишь для небольшой части задач. Эти решения достаточно часто содержат бесконечные ряды, специальные функции, трансцендентные уравнения для собственных значений и т.д. Все это значительно осложняет числовую оценку. На помощь приходят численные методы и наличие ЭВМ, обладающих большими быстродействием и памятью, позволяющие практически для любой инженерной задачи составить математическую модель и провести численное исследование. Идею численного метода можно понять на примере исследования распределения температуры в области, изображенной на рис.1.

Рис. 1

         Допустим, что для этого достаточно знать температуру в дискретных точках области. Одним из возможных методов является определение температуры в узловых точках сетки, на которую разбивается область. При этом для неизвестных значений температуры записываются и решаются алгебраические уравнения, а не дифференциальные. Именно это упрощение объясняет достаточно широкую доступность и применимость численных методов.

         Рассмотрим преимущества, недостатки и ограниченность каждого из трех перечисленных методов.

Экспериментальное исследование

         Необходимая и наиболее важная информация в этом случае получается при непосредственном “общении” с объектом исследования с природой. При этом вы в процессе исследования задаете интересующие вас вопросы объекту (природе) и через отклики, обеспечиваемые измерительной системой установки, получаете ответы от объекта (природы). С помощью постановки опытов на полномасштабной установке можно исследовать характер поведения объекта в натуральных условиях. Однако, в большинстве случаев такие полномасштабные опыты чрезмерно дороги и часто невозможны. Альтернативой является постановка модельного эксперимента. В этом случае натуральный объект должен быть заменен ему подобной с геометрической и физической точек зрения маломасштабной моделью. При этом проведение опытов необходимо осуществлять таким образом, чтобы была обеспечена возможность экстраполяции полученных результатов на натуральный объект и условия его воздействия с окружающей средой. Причем общие правила для этого процесса могут отсутствовать и должны быть установлены непосредственно исследователем, производящим опыты. На маломасштабных моделях не всегда возможно воспроизвести все свойства полномасштабного натурного образца. Часто приходится в объект, в изучаемую область вносить датчики. Это физические объекты с конкретными размерами и их появление вносит возмущение в процесс, а следовательно приводит к некоторому отличию протекания явления по сравнению с естественными условиями. Необходимо помнить, что в некоторых случаях измерения затруднены, а измерительная техника дает показания с некоторой погрешностью. Что касается аналитического метода, то его недостатки уже отмечались. Они прежде всего связаны с математическими трудностями постановочного характера и трудностями осмысления полученных решений, часто требующего самостоятельного дополнительного исследования.